Базовые правила (лингвистическая модель нечеткого статического преобразователя)
Правила, описывающие лингвистическую модель нечеткого статического преобразователя, могут использовать несколько лингвистических переменных, как в предпосылках, так и в заключениях правил. Поэтому контроллеры могут быть применимы как для задач управления в системах с одним входом и одним выходом (одномерными системами), так и для задач управления в системах с несколькими входами и несколькими выходами(многомерными системами). Типичная задача управления объектом с одним входом и одним выходом – изменять управляющее воздействие (управляющий сигнал), используя сигнал ошибки. При этом принцип управления называется управлением по ошибке (по отклонению). Для успешной работы контроллера могут потребоваться в качестве его (контроллера) входных сигналов не только сигнал ошибки, но и скорость изменения ошибки (производная от ошибки), и интеграл от ошибки. Однако их можно вычислить, используя одноконтурную систему управления, т.к. все три упомянутых переменных формируются из полученной в результате измерения ошибки. Ради простоты, в этом разделе предположим, что целью управления является регулирование (стабилизация) некоторой управляемой величины в соответствии с заданной рабочей точкой, другими словами, с заданным желаемым значением. Рассмотрение проблем построения правил, таким образом, ограничим лишь одноконтурными системами.
Пример. На рис. ниже показано, каким образом можно сформулировать правила, исходя из желаемой реакции системы на 1(t). Например, когда ошибка (e=1-y>0) и ее скорость изменения (ce=- 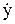 >0) положительны, то это означает, что управляемая величина уменьшается и удаляется от требуемого установившегося значения. Поэтому надо приложить к ОУ положительное управляющее воздействие (u>0). Путем подобных рассуждений приходим к четырем правилам:
>0) положительны, то это означает, что управляемая величина уменьшается и удаляется от требуемого установившегося значения. Поэтому надо приложить к ОУ положительное управляющее воздействие (u>0). Путем подобных рассуждений приходим к четырем правилам:
1. Если e>0 и ce>0, то u>0.
2. Если e>0 и ce<0, то u=0.
3. Если e<0 и ce>0, то u=0.
4. Если e<0 и ce<0, то u<0.
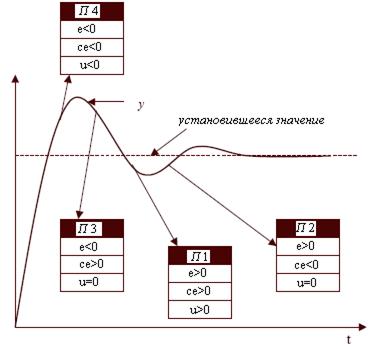
Рис. 2.6,a
Этих четырех правил достаточно, чтобы описать все возможные ситуации, которые представлены на рис. 2.6,a . Правило 1 описывает ситуацию, когда управляемая величина y меньше желаемого значения v, определяемого в данном случае ее установившимся значением, и продолжает уменьшаться (e>0 и ce>0). Очевидно, нужно, чтобы управляющее воздействие u (выходная величина регулятора) было положительным (u>0). Правило 4 имеет дело с противоположными обстоятельствами и, следовательно, выход регулятора должен быть отрицательным (u<0). Остаются еще два возможных ситуации (варианта действий): выход ОУ (управляемая величина) меньше установившегося значения, но ее значения увеличиваются (e>0 и ce<0); выход ОУ (управляемая величина) больше установившегося значения, но ее значения увеличиваются (e<0 и ce>0). В этих случаях желательно, чтобы управляющее воздействие оставалось на том же уровне в надежде на то, что выход ОУ сам по себе с течением времени медленно достигнет установившегося значения.
Еще одна возможность для формулировки правил связана с построением контроллера для управления нелинейной моделью, используя функцию Ляпунова. Пусть объектом управления служит одно звено робота, движение которого можно представить нелинейным дифференциальным уравнением
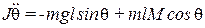 ,
,
где 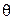 - угол отклонения звена относительно вертикали; M - момент, развиваемый двигателем постоянного тока;
- угол отклонения звена относительно вертикали; M - момент, развиваемый двигателем постоянного тока; 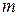 ,
, 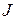 - соответственно масса и момент инерции звена;
- соответственно масса и момент инерции звена; 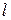 - длина звена. В этом примере цель управления состоит в обеспечении нулевого значения угла
- длина звена. В этом примере цель управления состоит в обеспечении нулевого значения угла 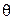 . При
. При 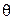 =0, полагая
=0, полагая 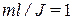 , получаем линеаризованное уравнение объекта
, получаем линеаризованное уравнение объекта
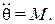
Обозначая 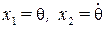 , запишем уравнения в переменных состояния
, запишем уравнения в переменных состояния

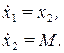
Для построения регулятора воспользуемся теорией устойчивости Ляпунова и рассмотрим в качестве кандидата на функцию Ляпунова положительно определенную функцию
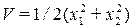 .
.
Для обеспечения устойчивости нулевого угла отклонения маятника производная от этой функции по времени
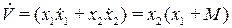
должна быть отрицательно определенной функцией, т.е. 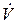 <0.
<0.
Рассмотрим случай 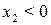 . Тогда
. Тогда 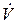 < 0, если
< 0, если 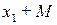
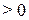 . Это условие применительно к моменту
. Это условие применительно к моменту 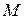 выполняется при
выполняется при 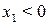 , если
, если 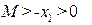 , и при
, и при 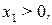 если
если 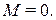 Рассмотрим теперь случай
Рассмотрим теперь случай 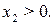 Тогда
Тогда 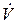 < 0, если
< 0, если 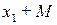
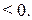 Последнее условие выполняется для
Последнее условие выполняется для 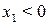 , если
, если 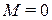 , и для
, и для 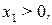 если
если 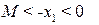 . Исходя их этих условий нетрудно придти к следующим правилам для нечеткого контроллера
. Исходя их этих условий нетрудно придти к следующим правилам для нечеткого контроллера
1. Если 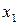 > 0 и
> 0 и 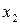 > 0, то
> 0, то 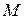 < 0.
< 0.
2. Если 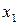 > 0 и
> 0 и 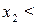 0, то
0, то 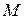 = 0.
= 0.
3. Если 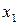
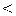 0 и
0 и 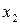 >0, то
>0, то 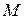 = 0.
= 0.
4. Если 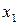
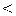 0 и
0 и 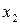
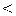 0, то
0, то 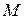 > 0,
> 0,
гарантирующим устойчивость нулевого состояния равновесия звена робота.

Лекция 9
Формы представления (форматы) правил. По сути дела нечеткий (лингвистический) контроллер содержит правила (нечеткую базу знаний или лингвистическую модель) в виде если – то, однако эти правила могут быть представлены в различных форматах. Во многих случаях для конечного пользователя правила представляют в формате, подобном приведенному ниже.
4. Если ошибка Отр и скорость изменения ошибки Отр, то выход ОтрБ.
5. Если ошибка Отр и скорость изменения ошибки Нуль, то выход ОтрС.
6. Если ошибка Отр и скорость изменения ошибки Пол, то выход Нуль.
7. Если ошибка Нуль и скорость изменения ошибки Отр, то выход ОтрС. (2.2)
8. Если ошибка Нуль и скорость изменения ошибки Нуль, то выход Нуль.
9. Если ошибка Нуль и скорость изменения ошибки Пол, то выход ПолС.
10. Если ошибка Пол и скорость изменения ошибки Отр, то выход ОтрБ.
11. Если ошибка Пол и скорость изменения ошибки Нуль, то выход ПолС.
12. Если ошибка Пол и скорость изменения ошибки Пол, то выход ПолБ.
Названия Нуль, Пол, Отр являются аббревиатурой названия нечетких множеств, так же как и названия ОтрБ, ОтрС, ПолБ, ПолС (отрицательное большое, отрицательное среднее, положительное большое и положительное среднее соответственно).
Второй формат – табличный лингвистический формат, более компактный. Входные переменные (сигналы) и их термы записывают вдоль сторон (верхней и левой боковой) таблицы, а термы выходной переменной – внутри таблицы.
 (2.3)
(2.3)
Если в таблице осталась пустая ячейка, это говорит о том, что пропущено одно из правил. Следовательно, такой формат полезен для оценки комплектности (полноты) правил. Когда входными сигналами являются ошибка и скорость изменения ошибки, этот формат называют лингвистической фазовой плоскостью. Если число используемых входных сигналов больше двух, т.е.
n > 2, таблица перерастает в n-мерный массив, очевидно, неудобный для пользователя.
Чтобы приспособить табличный формат на случай нескольких входных сигналов, вероятно, надо переделать ячейки таблицы. Надо отметить, что правило с несколькими выходными сигналами может быть разбито на совокупность нескольких правил, каждое с одним вспомогательным выходом.
Наконец, также можно использовать графический формат, который отображает функции принадлежности (рис. 2.8). Этот графический интерфейс пользователя отражает процесс инференции лучше, чем другие форматы, однако занимает много места на экране монитора.
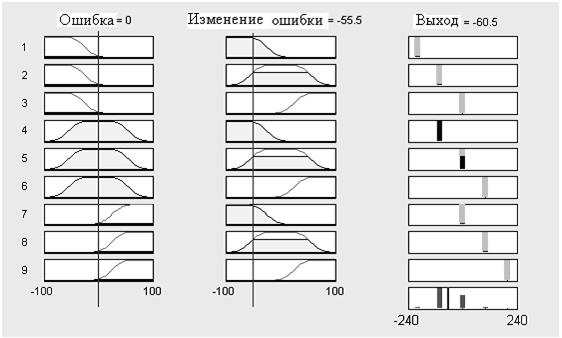
Рис. 2.8
Связки.Как вы уже знаете из первой главы, в математической логике предложения (высказывания) связывают словами и, или, если - то (или импликацией) и если и только если или их модификациями, образуемыми с помощью слова не. Эти пять слов называются связками (соединениями). Также очень важно как реализуются связки в математическом смысле. Вероятно, наиболее известна операция умножения (алгебраического произведения) для нечеткого и, используемая вместо операции минимум (min). До сих пор большинство приведенных примеров включают лишь операторы и, но правила, подобные «Если ошибка большая отрицательная и не равна нулю или скорость изменения ошибки равна нулю, то… », также возможны.
Связки (соединения) и и или всегда определяются попарно, например,
a и b =min(a, b) минимум
a или b =max(a, b) максимум
или (2.4)
a и b = a* b алгебраическое произведение
a или b = a+ b - a* b алгебраическая или вероятностная сумма.
Можно привести другие примеры реализации связок, но они являются более сложными.
Выбор универсума. Элементы нечеткого множества берутся из универсального множества или универсума. Универсум содержит все элементы, которые могут быть приняты к рассмотрению. Прежде чем конструировать функции принадлежности, необходимо выбрать универсумы для входных и выходных переменных (сигналов) контроллера. Например, рассмотрим правило
Если ошибка Отр и скорость изменения ошибки Пол, то выход равен Нуль .
Естественно, функции принадлежности для Отр и Пол должны быть определены для всех возможных значений ошибки и скорости изменения ошибки, и может быть пригоден стандартный универсум [-100, 100]. Универсум – по сути, область определения нечеткого множества.
Другой проблемой, достойной обсуждения, является вопрос о том, должна ли быть функция принадлежности непрерывной или дискретной. Непрерывная функция принадлежности определена на непрерывном универсуме значений входа/выхода. Дискретная функция принадлежности определена в рамках вектора с конечным числом элементов. В последнем случае необходимо установить (выбрать) диапазон универсума и значения в каждой его дискретной точке. Выбор между малым или большим разрешением (шагом квантования по уровню) есть компромисс между требованиями точности, быстродействия и пространства, занимаемого на мониторе. Если квантователь затрачивает много времени на выполнение предписанных ему функций и обусловленное этим обстоятельством время задержки имеет большое значение, надо использовать непрерывные функции принадлежности, т.е. надо отказаться от применения квантователя.
Пример 2.1 (стандартные универсумы). Многие авторы и коммерческие контроллеры используют стандартные универсумы.
· Нечеткий контроллер Шмидта (Fl Smidth), например, использует диапазон вещественных чисел [-1,1].
· Авторы ранних работ по нечеткому управлению использовали целые числа из диапазона [-6, 6].
· Другая возможность применить диапазон [-100, 100], соответствующий полной процентной шкале (полной шкале в процентах).
· Еще одна возможность – диапазон целых чисел [0, 4095], соответствующий выходу двенадцатиразрядного АЦП.
· Вариантом последней рассмотренной возможности служит диапазон
[-2047, 2048], смещенный относительно диапазона [0, 4095] с целью учесть отрицательные целые числа.
Выбор типа данных может обусловить выбор универсума. Например, диапазон [-5, 5] в вольтах может быть представлен как диапазон целых чисел
[-50,50] или как диапазон чисел с плавающей запятой [-5.0, 5.0], тип данных со знаковым разрядом (битом) приводит к диапазону целых чисел [-128,127].
Лучший путь для использования всего диапазона универсума применить масштабирование входов/выходов. Если вход контроллера содержит лишь один терм, то с помощью выбора масштабирующего коэффициента можно добиться использования в процессе работы всего диапазона универсума. Преимущество такого подхода состоит в том, что он позволяет использовать стандартный универсум, что исключает необходимость добавления новых термов.
Выбор функций принадлежности. Напомним, что каждый элемент универсума является в то же время элементом нечеткого множества с некоторой степенью, может быть даже нулевой. Степени принадлежности, заданные для всех элементов нечеткого множества, полностью описывают нечеткое множество, например, такое, как Отр. Элементам нечетких множеств присваивают степени принадлежности так, чтобы переход от членства (принадлежности) к не членству (не принадлежности) был скорее постепенным, чем скачкообразным. Совокупность элементов с ненулевой степенью принадлежности называют опорой для нечеткого множества. Функция, которая ставит в соответствие каждому элементу универсума определенное числовое значение, называется функцией принадлежности 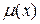 .
.
Проектировщик системы неизбежно сталкивается с вопросом как построить (выбрать) терм-множество. При этом в сущности надо ответить на два вопроса: 1) Какой вид должны иметь функции принадлежности термов?
2) Какое число термов является необходимым и достаточным? Например, лингвистическая переменная ошибка применительно к контроллеру использует семейство термов (терм-множество) Отр, Нуль и Пол. Согласно теории нечетких множеств выбор формы и числа терм является субъективным решением, другими словами, определяется опытом и интуицией проектировщика, однако в любом случае применимы следующие эмпирические правила.
· Число термов должно быть достаточно большим, чтобы допустить присутствие шума в измерениях.
· Желательно иметь некоторое число пересечений (перекрытий) функций принадлежности термов; иначе контроллер может не получить достаточного объема информации, необходимого для формирования эффективного управляющего воздействия.
Предварительный ответ на вопросы (1) и (2) звучит так: необходимое и достаточное число элементов терм-множества зависит от ширины основания (опоры) функций принадлежности термов и наоборот. Один из возможных путей решения данной задачи – опрос операторов технологического процесса (объекта управления) с целью учесть их мнение при выборе кривых для функций принадлежности терм. Хотя следует сказать, что операторы обычно также затрудняются с ответом на вопрос о требуемом виде кривых для функций принадлежности.
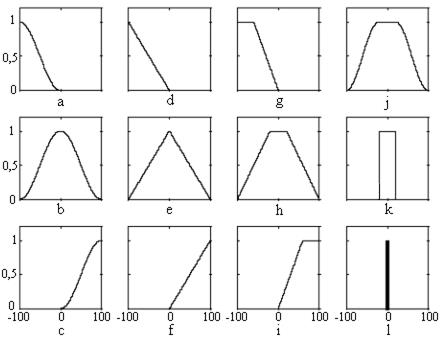
Рис. 2.7
Некоторые авторы рекомендуют следующий подход.
· Начать конструирование с треугольных функций принадлежности. Все функции принадлежности (ФП) для конкретных входов/ выходов должны быть симметричными треугольниками одной и той же ширины (одного и того же основания) вида (e). Крайние левая и правая ФП должны быть функциями вида (d) и (f) (рис. 2.7).
· Перекрытие ФП между собой должно составлять не менее 50 %. Ширина (основание) треугольников должно быть выбрано так, чтобы каждое значение универсума было членом (элементом) по меньшей мере, двух множеств, исключая, пожалуй, элементы на самых концах диапазона (см. рисунок ниже).
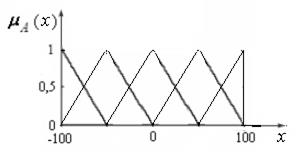
С другой стороны, надо отметить, что если имеется разрыв между соседними ФП, ни одно из правил не работает при всех значениях входа/выхода, принадлежащих этому разрыву. Следовательно, контроллер не знает, что ему делать.
На рис. 2.7 приведены примеры некоторых типичных функций принадлежности. Читая сверху вниз, слева направо: (a) s - функция, (b) 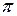 - функция, (с) z - функция, (d–f) различные версии треугольной функции, (g–i) различные версии трапецеидальной функции, (j)
- функция, (с) z - функция, (d–f) различные версии треугольной функции, (g–i) различные версии трапецеидальной функции, (j) 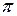 - функция с плоской вершиной, (k) прямоугольная функция, (l) синглтон.
- функция с плоской вершиной, (k) прямоугольная функция, (l) синглтон.
Функции принадлежности могут быть с плоскими вершинами, кусочно-линейными и треугольной формы, или наклонными с горизонтальными уступами вида (g) и (i).
Речь выше шла о выборе функций принадлежности для условий (антецедентов). Теперь обратимся к выбору функций принадлежности для заключений (консеквентов).

Рис. 2.7
Лекция 9
Напомним, что нечеткое множество 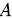 представляет собой набор упорядоченных пар
представляет собой набор упорядоченных пар
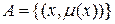 . (2.5)
. (2.5)
Здесь элемент x принадлежит универсуму и 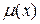 есть его степень принадлежности к множеству
есть его степень принадлежности к множеству 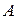 . Отдельно взятая пара
. Отдельно взятая пара 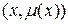 называется нечетким синглтоном, другими словами, одноточечным множеством или множеством, состоящим из одного элемента. Использование в качестве выходного сигнала контроллера синглтона (singleton output) означает, что нечеткое множество в консеквенте (заключении) правил заменяется четким числом (скаляром), например, так.
называется нечетким синглтоном, другими словами, одноточечным множеством или множеством, состоящим из одного элемента. Использование в качестве выходного сигнала контроллера синглтона (singleton output) означает, что нечеткое множество в консеквенте (заключении) правил заменяется четким числом (скаляром), например, так.
1. Если ошибка есть Пол, то выход равен 10 вольтам.
2. Если ошибка есть Нуль, то выход равен 0 вольтам. (2.5,а)
3. Если ошибка есть Отр, то выход равен -10 вольтам.
Модель, описываемая правилами, подобными (2.5,а), называют синглтонной моделью.
Использование в качестве выхода синглтона обладает следующими достоинствами:
· упрощаются вычислительные операции;
· можно свести весь диапазон значений управляющего сигнала к крайним значениям этого диапазона;
· такое решение может быть актуальным как интуитивный путь написания правил.
Скаляр (четкую переменную) можно рассматривать как нечеткое множество с синглтоном, расположенным на соответствующей позиции. Например, 10 вольт должно быть эквивалентно нечеткому множеству, определенному на универсуме [-10 -5 0 5 10] с функцией принадлежности (0 0 0 0 1). Используя дискретную 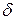 - функцию (символ Кронекера), функцию принадлежности для такого синглтона можно записать как
- функцию (символ Кронекера), функцию принадлежности для такого синглтона можно записать как
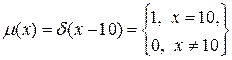 . (2.6)
. (2.6)
Пример 2.2 (Функция принадлежности). При проектировании нечетких контроллеров используются различного вида функции принадлежности. Обобщенным примером функции, которая графически имеет вид колокола, является экспоненциальная функция, называемая иногда колоколообразной,
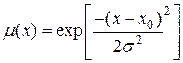 . (2.7)
. (2.7)
Это стандартная гауссовская кривая с максимальным значением 1, 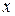 есть независимая переменная, заданная на универсуме,
есть независимая переменная, заданная на универсуме, 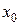 есть положение максимума кривой относительно универсума, и
есть положение максимума кривой относительно универсума, и 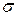 есть среднеквадратическое отклонение. Другая функция, которая не использует экспоненту, имеет вид
есть среднеквадратическое отклонение. Другая функция, которая не использует экспоненту, имеет вид
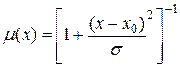 . (2.8)
. (2.8)
В нечетком контроллере Шмидта используется функция
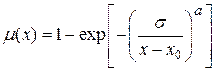 . (2.9)
. (2.9)
Дополнительная переменная 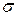 определяет градиент спадания до нуля боковых сторон графика этой функции. Также можно использовать другие функции, например, сигмоидальную функцию, широко используемую в искусственных нейронных сетях, или рассмотренные в первой главе функции принадлежности в виде s- кривой, z- кривой и
определяет градиент спадания до нуля боковых сторон графика этой функции. Также можно использовать другие функции, например, сигмоидальную функцию, широко используемую в искусственных нейронных сетях, или рассмотренные в первой главе функции принадлежности в виде s- кривой, z- кривой и 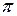 - кривой.
- кривой.
Дата добавления: 2021-01-11; просмотров: 896;











