Отношения между нечеткими множествами

В любом нечетком контроллере отношения между множествами играют главную роль. Понятие нечеткого отношения, наряду с понятием самого нечеткого множества, следует отнести к фундаментальным основам всей теории нечетких множеств. Нечеткое отношение часто заменяется терминами нечеткая связь, ассоциация, взаимосвязь или соотношение. Некоторые отношения затрагивают элементы одного и того же универсума: например, одно измерение больше другого, одно событие наступает раньше другого, один элемент похож на другой элемент и т.п. Другие отношения связывают элементы из разных универсумов, например величина измерения большая и его скорость изменения положительная, x- координата (абсцисса) большая и y- координата (ордината) малая. В этих примерах фигурируют отношения между двумя множествами. Однако в принципе могут иметь место отношения, устанавливающие связи между несколькими множествами.

Формально бинарное четкое отношение или просто четкое отношение R между двумя четкими множествами 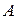и (отношение между элементами x и y множеств 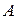и ) приписывает каждой упорядоченной паре 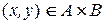только лишь одно из следующих утверждений: а) «x связано с y» или б) «x несвязано с y». Продукционное пространство или декартово произведение множеств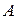 есть множество всех возможных комбинаций (пар) элементов (значений) из 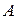и или это то же, что для всех 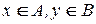, т.е.

.

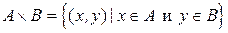Нечеткое отношение R между множествами A и , называемое бинарным (двумерным) нечетким множеством, есть нечеткое подмножество декартового произведения 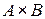соответствующих этим множествам универсумов A и B. При этом двумерная функция принадлежности 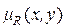, описывающая нечеткое отношение, показывает степень выполнения отношения

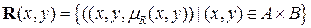
между элементами x и y, ,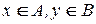

Отсюда нечеткие отношения являются более гибкими по сравнению с традиционными (четкими) отношениями. Они позволяют задавать не только сам факт выполнения соотношений, но и указывать степень его выполнения, что является очень важным для многих практических задач, в частности для задач управления.

Нечеткое отношение R между множествами A и называют бинарным (двумерным) нечетким множеством с функцией принадлежности 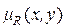. Если множество A состоит из m элементов, а множество из элементов, то 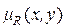является матрицей размерности ( 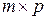). По сути дела нечеткое отношение можно считать равным своей функции принадлежности 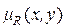, т.е. можно записать, что .

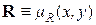Пример 1. R:x 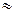y ( x приблизительно равно y). При этом

.

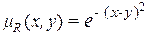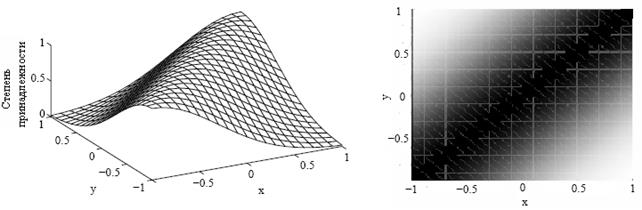
Пример 2. Еще один пример функции принадлежности 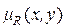нечеткого отношения R в случае, когда имеет место треугольная функция принадлежности для A и трапециидальная функция принадлежности для B, показан на рисунке ниже.

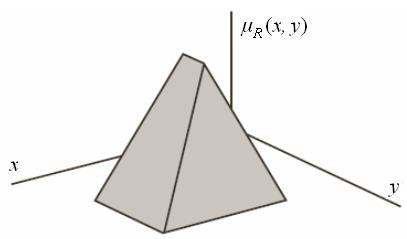
Пример 3. Предположим, например, что племянник Ивана Соколова Владимир похож на другого племянника Бориса со степенью 0,8, и Владимир похож со степенью 0,9 на третьего племянника Николая. Отсюда имеет место отношение между подмножествами племянников в семье. Его удобно представить в виде матрицы (с одной строкой)

Здесь мы рассматриваем отношение «Владимир похож на других племянников». Нечеткое множество A состоит из одного элемента 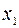= =Владимир, нечеткое множество из двух элементов 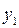= Борис и 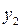= =Николай. Функция принадлежности

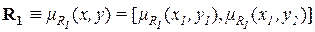=[0,8 0,9]

задает отношение между множествами A и B.

Композиция. Для того чтобы показать, каким образом два отношения могут быть представлены как их комбинация (композиция), пропишем еще отношение между Борисом и Николаем, с одной стороны, и Иваном Соколовым − с другой в виде матрицы (с одним столбцом)

Здесь мы рассматриваем отношение «Племянники Борис и Николай похожи на Соколова». Нечеткое множество C состоит из одного элемента 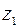= Соколов, нечеткое множество из двух элементов 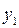= Борис и 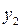= Николай. Функция принадлежности для отношения 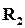между множествами и C имеет вид матрицы с одним столбцом

= .

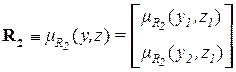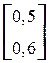Заманчиво теперь найти ответ на вопрос, насколько похож Владимир на Ивана Соколова, другими словами, найти отношение «Владимир похож на Соколова» или отношение

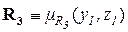
между A и C путем комбинации сведений, приведенных в двух указанных матрицах:

а) Владимир похож со степенью 0,8 на Бориса, и Борис похож со степенью 0,5 на Соколова;

б) Владимир похож со степенью 0,9 на Николая, и Николай похож со степенью 0,6 на Соколова.

Утверждение (высказывание) “а” содержит последовательную цепочку (связь) отношений (рис. 1.4,а) и, по-видимому, резонно объединить их (отношения) с помощью операции пересечение. В соответствии с данным нами определением операции пересечение она здесь сводится к выбору наименьшего значения степени принадлежности для отношения Владимир – Соколов, т.е. 0,5. Аналогично поступаем с отношением “б”. Осуществляя описанные операции применительно к последовательным цепочкам (связям) “а” и “б”, получаем параллельную цепочку (связь) (рис. 1.4,б)

в) Владимир похож со степенью 0,5 на Соколова.

г) Владимир похож со степенью 0,6 на Соколова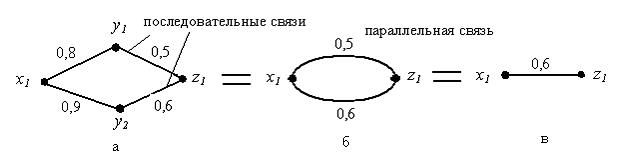

Полученные отношения “в” и “г” кажутся одинаково обоснованными, однако, по-видимому, разумно применить операцию объединение, чтобы получить единственный ответ. В соответствии с данным нами определением операции объединение она в данном случае сводится к выбору наиболее сильной связи, т.е. к выбору наибольшего значения (максимума) степени принадлежности. Окончательный результат, представленный на рис. 1.4,в, надо трактовать как

д) Владимир похож со степенью 0,6 на Соколова.

Визуальное изображение отношений и композиции с помощью графов показано на рис. 1. 4.

Общее правило, когда осуществляется комбинация или, другими словами, композиция нечетких отношений, выбрать минимальное значение в «последовательной связи (цепи)» и максимальное значение в «параллельной связи (цепи)». Эти операции удобно реализовать, используя внутреннее произведение.

Лекция 4

Внутреннее произведение сходно с обычным произведением матриц (символ точка) за исключением того, что операция умножения заменяется пересечением 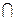, а операция суммирования заменяется объединением 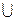. Предположим, что R – матрица m 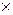p, а S– матрица p 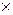n. Тогда внутреннее произведение T= 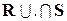есть матрица T= [ 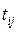] размерности m 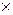n, каждый (ij)- элемент 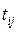которой находится путем комбинации i- строки матрицы R и j- го столбца матрицы S,так что

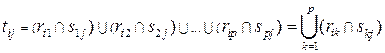, (1.7)

т.е. i- строка матрицы R«умножается» на j - й столбец матрицы S с использованием операции 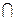, затем полученный результат «свертывается» в 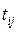с помощью операции .

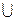В соответствии с данными нами определениями операциям пересечение как операции minи объединение как операции max выражение (1.7) можно записать в виде

. (1.8)

Композиция, описываемая последним выражением, в литературе называется max-min композицией (максиминной композицией).

Если R есть нечеткое отношение между множествами A и 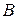, и S есть нечеткое отношение между множествами 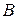и C , то композиция (свертка) R и S есть нечеткое отношение между A и C [свойство транзитивности (переходности)], так что

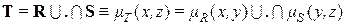
Пример 1.8 (внутреннее произведение). Для отношени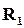й и 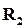, представленных таблицами

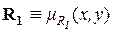=[0,8 0,9],

= ,

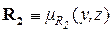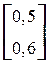приведенными выше на с. 14, 15, получаем

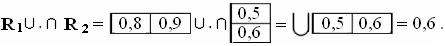
что совпадает с полученным выше результатом.

Максиминная композиция дистрибутивна по отношению к операции объединение,

,

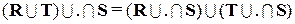но не по отношению к операциипересечение. Иногда в выражении (1.8) для максиминной композиции обозначение операции min заменяют *, используемой для обозначения операции алгебраического умножения. Тогда такую композицию называют max-star композицией или чаще max-prod композицией.

Заметим, что при проектировании нечетких контроллеров часто используется композиция между нечетким множеством A и отношением R

,

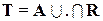тогда T представляет вектор-строку.

Находит применение композиция между двумя множествами A и B

,

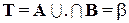где 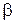- постоянная величина.

Нечеткая логика

Логика начиналась с изучения естественного языка с точки зрения аргументов и убеждений и могла быть использована для суждения о корректности цепи высказываний, например в математических доказательствах. Заметим, что высказывание - мысль, выраженная повествовательным предложением и являющаяся истинной или ложной, а истина - адекватное отображение предметов и явлений познающим субъектом. В двухзначной (точной) логике высказывание является верным (истинным) или неверным (ложным), но не тем и другим. «Истина» или «ложь», приписываемые высказыванию, называются истинностными значениями (значениями истинности). В нечеткой логике нечеткое высказывание может быть верным или неверным или иметь промежуточные истинностные значения, например, может быть верно. Высказывание уровень высокий является примером такого высказывания в нечетком контроллере. По-видимому, удобно ограничить возможные истинностные значения в дискретной области, скажем значениями {0 0,5 1} для ложно, может быть верно, верно. В таком случае мы будем иметь дело с многозначной логикой, в данном случае, с трехзначной логикой. На практике разделение единичного интервала на меньшие части может быть более подходящим. При этом интервал {0 1} включает множество значений истинности нечетких высказываний.

Изначально Задэ интерпретировал значение истинности в нечеткой логике, например, Очень точно, как нечеткое множество. Таким образом, Задэ заложил в основание нечеткой (лингвистической) логики трактовку Истины как лингвистической переменной, значениями которой являются скорее слова или высказывания, чем числа.