Графическая интерпретация операций импликации и инференции для непрерывных универсумов
Композиционное правило инференции является обобщением следующего известного понятия. Предположим, что мы имеем функцию y =f(x), которая определяет отношения между интервальными переменными, как показано на рисунке ниже. Чтобы найти результирующий интервал y=b, соответствующий интервалу x=a, мы вначале создаем цилиндрическое расширение a (т.е. расширяем область a из линии X на плоскость X 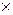 Y) и затем находим его пересечение I с графиком интервальной зависимости. Проекция I на ось y определяет искомый интервал y=b.
Y) и затем находим его пересечение I с графиком интервальной зависимости. Проекция I на ось y определяет искомый интервал y=b.
Обобщим эту графическую интерпретацию на операции импликации и инференции.
Пусть бинарное нечеткое отношение 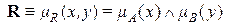 определено в декартовом пространстве X
определено в декартовом пространстве X  Y непрерывных универсумов X и Y как пересечение множеств A и B . Тогда функция принадлежности
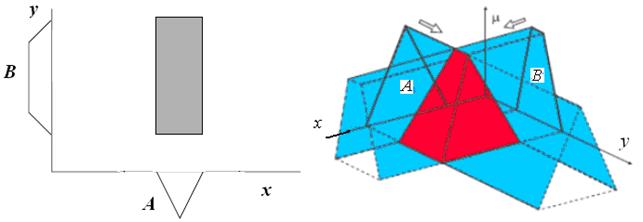
Y непрерывных универсумов X и Y как пересечение множеств A и B . Тогда функция принадлежности 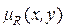 нечеткого отношения R может быть представлена как поверхность в трехмерном пространстве. В качестве примера на рис. 1.5,а показана такая поверхность для треугольной функции принадлежности
нечеткого отношения R может быть представлена как поверхность в трехмерном пространстве. В качестве примера на рис. 1.5,а показана такая поверхность для треугольной функции принадлежности 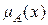 для A и трапециидальной функции принадлежности
для A и трапециидальной функции принадлежности 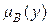 для B.
для B.
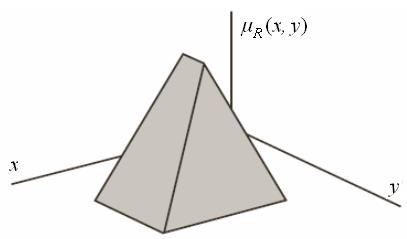
Рис. 1.5,а
Остановимся на том, каким образом получено графическое представление нечеткого отношения между множествами A и B, для которых известны их функции принадлежности 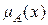 и
и 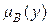 .
.
Прежде всего, заметим, что двумя важными операциями на нечетких множествах и нечетких отношениях являются проекция и цилиндрическое расширение. Операция проекция преобразует тернарное отношение(отношение трех нечетких множеств) в бинарное, или бинарное отношение в нечеткое множество, или нечеткое множество в четкое единственное значение.
В бинарном случае проекция R на Y (полагаем, что R определено на X  Y) определяется как
Y) определяется как
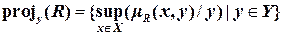 .
.
В результате этой операции над нечетким отношением, представленным функцией принадлежности, изображенной на рис. 1.5,а, получаем проекцию (тень) Rна Y в виде множества B (рис. 1.5,б).
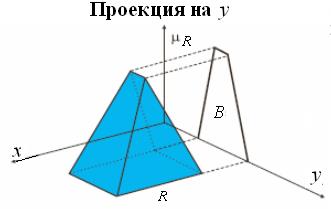
Рис. 1.5,б
Аналогичным образом определяется проекция (тень) R на X в виде выражения
и в виде множества A (рис. 1.5,в).
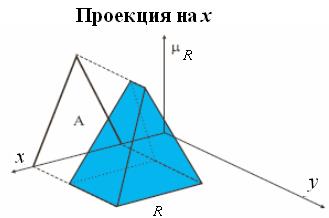
Рис. 1.5,в
Вместо оператора супремум (supremum, верхняя грань), который необходим, когда универсумы X и Y являются непрерывными, для дискретных универсумов используют оператор max.
Лекция 6
Операция проекция почти всегда применяется в комбинации с цилиндрическим расширением. Цилиндрическое расширение до некоторой степени противоположно проекции. Эта операция расширяет нечеткое множество до нечеткого бинарного отношения, нечеткое бинарное отношение до нечеткого тернарного отношения, и т. д. В бинарном случае (пусть нечеткое множество A определено на универсуме X) цилиндрическое расширение A на X  Y является множеством всех кортежей (упорядоченных пар) (x,y)
Y является множеством всех кортежей (упорядоченных пар) (x,y) 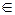 X
X 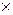 Y со степенью принадлежности
Y со степенью принадлежности 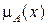 , т.е.
, т.е.
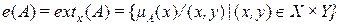
или
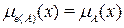 .
.
Такое цилиндрическое расширение для треугольной функции принадлежности 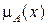 представлено на рис. 1.5, г.
представлено на рис. 1.5, г.
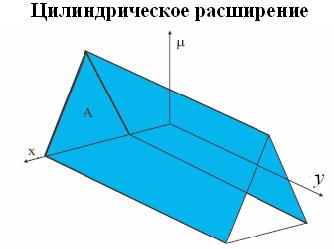
Рис. 1.5, г
Для заданных нечетких множеств A и B непосредственнонельзя найти графическое представление их отношения. Однако если A расширено на X  Y, т.е. получено
Y, т.е. получено 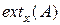 , и B расширено на X
, и B расширено на X 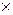 Y, т.е. получено
Y, т.е. получено 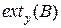 , то такое представление оказывается возможным (рис. 1.5,д). Здесь
, то такое представление оказывается возможным (рис. 1.5,д). Здесь
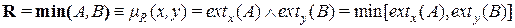 .
.
Пример. A  B на X
B на X  Y .
Y .
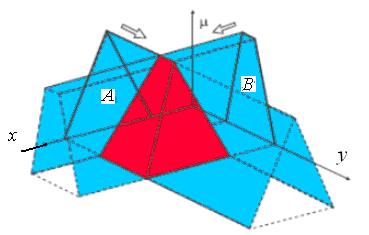
Рис. 1.5,д
В результате расширения множеств A и B и последующего выполнения операции пересечения этих расширений мы получаем в виде поверхности двумерную ФП для нечеткого отношения (показана красным цветом).
Операции цилиндрического расширения и пересечения служат главным образом для следующей цели: пусть  является нечетким множеством, определенном на X, и пусть R является нечетким отношением множеств A и B, определенном на X
является нечетким множеством, определенном на X, и пусть R является нечетким отношением множеств A и B, определенном на X 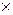 Y . При этом конечно, нельзя найти пересечение
Y . При этом конечно, нельзя найти пересечение 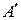 и R, однако, если
и R, однако, если 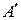 расширено на X
расширено на X 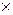 Y, то определить такое пересечение оказывается возможным. Другими словами, при этом можно найти
Y, то определить такое пересечение оказывается возможным. Другими словами, при этом можно найти
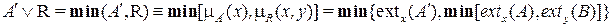 .
.
Таким образом, мы получаем нечеткое отношение 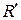 =
= 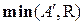 , другими словами, пересечение цилиндрического расширения
, другими словами, пересечение цилиндрического расширения 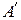 и отношения R, связывающее нечеткие множества
и отношения R, связывающее нечеткие множества 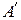 и
и 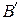 с функциями принадлежности
с функциями принадлежности 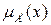 и
и 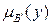 соответственно, т.е.
соответственно, т.е.
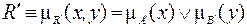 .
.
(Сравните с графиком интервальной зависимости, рассмотренным ранее.)

Теперь функцию принадлежности 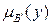 нечеткого множества
нечеткого множества 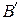 можно найти как проекцию
можно найти как проекцию 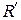 на y
на y
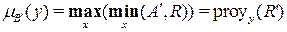 .
.
Следовательно, приходим к нечеткому логическому выводу  , представленному в графической форме (рис. 1.5,е).
, представленному в графической форме (рис. 1.5,е).
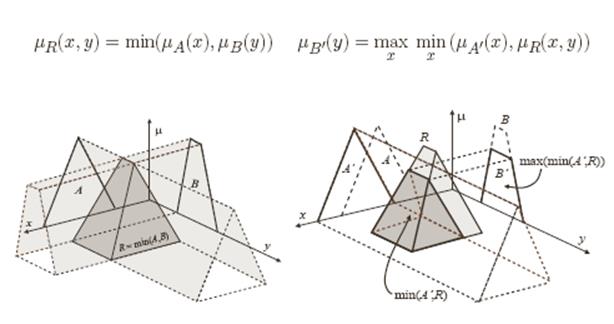
Рис.1.5,е
Несколько правил
Базовые правила обычно содержат несколько правил. Остановимся на том, каким образом мы их объединяем. Обратимся к простым базовым правилам
Если уровень есть НИЗКИЙ (A1), то сигнал (V1) есть ОТКРЫТЬ (B1) (1.21)
Если уровень есть ВЫСОКИЙ (A2), то сигнал (V1) есть ЗАКРЫТЬ (B2).
и найдем лингвистическую модель, связывающую переменные уровень и входной сигнал вентиля,
Мы неявно предполагаем наличие связки илимежду правилами, так что отношение между предпосылкой и заключением правил записывается, как R1 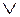 R2, где
R2, где
R1 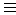 низкий
низкий 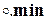 открыть
открыть
есть импликация 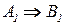 для первого, а
для первого, а
R2 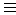 высокий
высокий 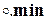 закрыть
закрыть
− импликация 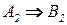 для второго правила. Нечеткое отношение R,представляющее оба правила (1.21), вычисляется как логическое илидвух таблицдляR1 и R2 элемент за элементом (поэлементный максимум). В общих обозначениях для N правил, мы имеем
для второго правила. Нечеткое отношение R,представляющее оба правила (1.21), вычисляется как логическое илидвух таблицдляR1 и R2 элемент за элементом (поэлементный максимум). В общих обозначениях для N правил, мы имеем
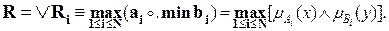 .
.
Теперь все правила отображаются как одно нечеткое множество Rи выход лингвистической модели представляет собой максиминную композицию
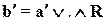 .
.
При этом инференция осуществляется над отношением R.
Пример 1.14 (ОМР, два правила). Дополним рассмотренное в примере 1.12 правило «Если уровень есть НИЗКИЙ, то входной сигнал V1 вентиля ОТКРЫТЬ»с термами (нечеткими множествами) НИЗКИЙ(A1) и ОТКРЫТЬ(B1), определяемыми c помощью дискретных функций принадлежности как
а1= низкий = [1 0,75 0,5 0,25 0]
b1= открыть = [0 0,5 1],
еще одним правилом «Если уровень есть ВЫСОКИЙ, то входной сигнал V1 вентиля ЗАКРЫТЬ»с переменными (нечеткими множествами) ВЫСОКИЙ (A2) и ЗАКРЫТЬ (B2), определяемыми c помощью дискретных функций принадлежности как
a2= высокий = [0 0,25 0,5 0,75 1]
b2=закрыть = [1 0,5 0].
Нечеткое отношение R1  низкий
низкий 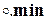 открыть, другими словами,импликация
открыть, другими словами,импликация 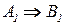 для первого правила определяется выражением (1.13а), т.е.
для первого правила определяется выражением (1.13а), т.е.

а нечеткое отношение R2  высокий
высокий 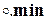 закрыть − импликация
закрыть − импликация 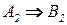 для второго правила в соответствии с (1.13) вычисляется по следующей схеме
для второго правила в соответствии с (1.13) вычисляется по следующей схеме
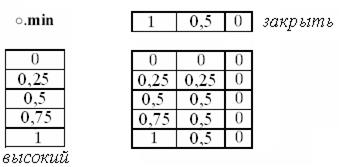 .
.
Отсюда
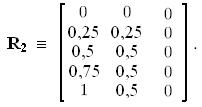

Нечеткое отношение R= R1 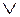 R2 есть логическое илидвух отношений R1иR2 элемент за элементом (поэлементный максимум):
R2 есть логическое илидвух отношений R1иR2 элемент за элементом (поэлементный максимум):

Графическая визуализация этих шагов представлена на рис. 1.6.
В MATLAB 6.5 /work/script1/plotreal.m
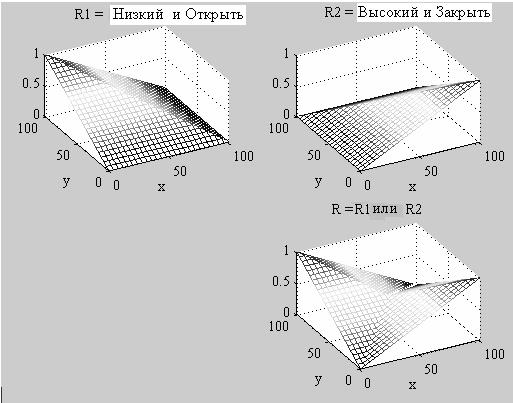
Рис. 1.6
Изображенные на этом рисунке отношения вычисляются с помощью значительно меньшего шага квантования сигналов «уровень» и «входной сигнал вентиля», обозначенных соответственно как x и y, по сравнению с функциями принадлежности aiиbi, (i=1,2). Т.е. путем использования дискретных функций принадлежности, получаемых из непрерывных функций принадлежности (рис. 1.7), путем более «частого» квантования.
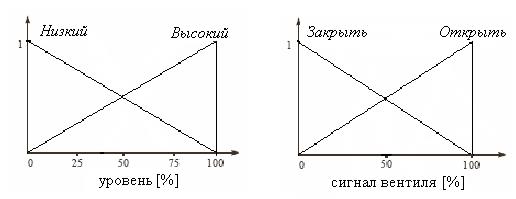
Рис. 1.7
В соответствии с полученным изображением отношения Rлингвистическая модель, связывающая сигналы y и x, называется нечетким графом. Рис. 1.8 показывает нечеткий граф для нашего примера (другими словами, изолинии для R, где степень затемнения соответствует степени принадлежности). Самые темные участки
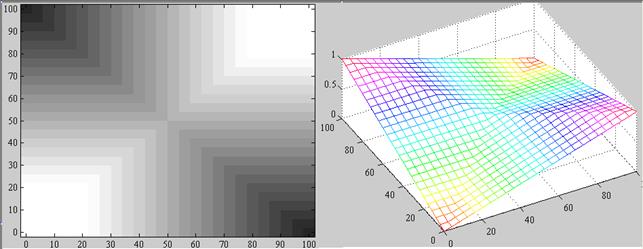
Рис. 1.8
говорят о том, что значения y и x связаны со степенью 1, более светлые свидетельствуют о более слабой связи.
Нечеткую композицию
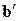 = v1 =
= v1 = 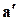
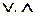 R
R
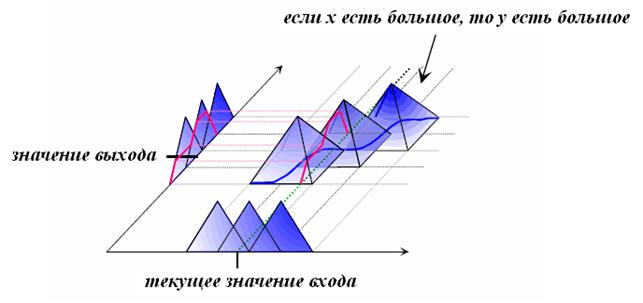
можно трактовать как вычисление значения функции на нечетком графе, а последний как нечеткую функцию. На рис. 1.9 дана геометрическая интерпретация вычисления значений нечеткой функции при четком (синглтон) и нечетком (нечеткое множество) аргументах в самом общем случае.
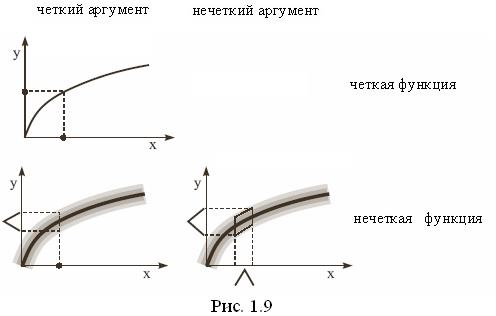
Для рассматриваемого примера возможную четкую функцию, отражающую связь y и x, можно представить в виде сплошной прямой (рис. 1.8).
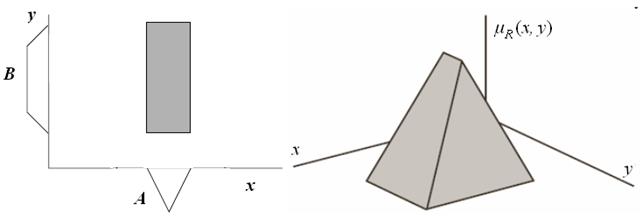
Пример 1. Если x есть A , то y есть B.
Пример 2.
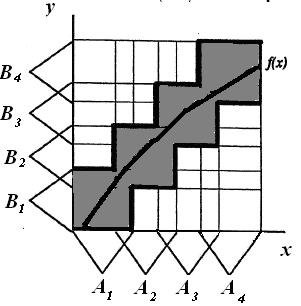
Если x есть A1 , то y есть B1 ,
Если x есть A2 , то y есть B2 ,
Если x есть A3 , то y есть B3 ,
Если x есть A4 , то y есть B4 .
Дата добавления: 2021-01-11; просмотров: 669;











