Функции принадлежности

Каждый элемент в универсуме является членом (элементом) нечеткого множества A с некоторой степенью принадлежности, может быть и с нулевой.

ФП является просто степенью, с которой элемент x принадлежит к множеству A. ФП 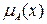преобразует универсум U в интервал [0,1],

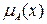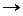: U [0,1],

т.е. каждому элементу x универсума U ставит в соответствие определенное число из интервала [0,1]. Если 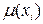=0,8, то говорят, что элемент x_i на 80% принадлежит нечеткому множеству A.

Нечеткое множество строго определяется с помощью функции принадлежности, другими словами, логика определения понятия нечеткого множества не содержит никакой нечеткости. Четкое множество является частным случаем нечеткого множества, т.е. понятие нечеткого множества является расширенным понятием, охватывающим понятие четкого множества.

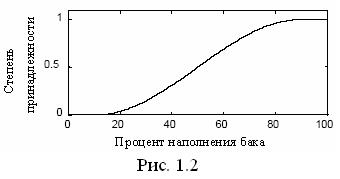
Непрерывное и дискретное представления. Существуют два альтернативных представления функций принадлежности в компьютере: непрерывный и дискретный. В непрерывной форме функция принадлежности есть математическая функция, возможно программа. Функция принадлежности может быть колоколообразной (так называемая 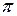- кривая), s-образной (называемая s-кривой), обратная s-образной (называемая z-кривой), треугольной или трапециидальной. На рис. 1.2 изображена как пример 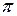- кривая. В дискретной форме функция принадлежности и универсум представляют собой дискретные значения (точки) в списке (векторе). В ряде случаев удобно иметь дело с дискретными представлениями.

В соответствии с эмпирическим правилом непрерывная форма требует более быстродействующего, но с меньшей памятью АЦП, чем дискретная форма.

Пример 1.4 (непрерывная форма). Функция косинуса может быть использована для построения различных функций принадлежности. Так s-кривая может быть описана как

, (1.3)

где a_l - левая точка излома, а a_r- правая точка излома кривой. z-кривая является зеркальным отражением s-кривой относительно точки (a_r- a_l)/2:

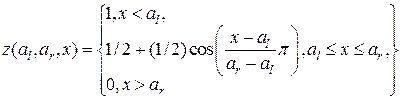. (1.4)

При этом 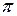- кривая может быть интерпретирована как комбинация s-кривой и z-кривой, тогда в интервале [a₂, a₃] при условии 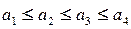значения функции принадлежности

(1.5)

одинаковы и максимальны.

На рис. 1.2 изображена 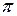- кривая, описываемая функцией

.

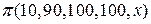Пример 1.5 (дискретная форма). Чтобы получить дискретное представление, эквивалентное кривой, изображенной на рис. 1.2, предположим, что универсум U= u представлен дискретными значениями, скажем такими

u =[0 20 40 60 80 100].

Занесем результаты вычислений по формулам (1.3), (1.4) и (1.5) в соответствующий список значений

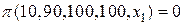
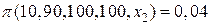
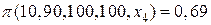
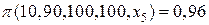
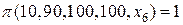
или в кратком виде,

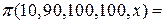[ 0 0,04 0,31 0,69 0,96 1 ].

Кстати, символически принято нечеткое множество на универсуме записывать как множество упорядоченных пар,

для непрерывных и дискретных универсумов соответственно. Здесь символы и не имеют никакого отношения к операциям интегрирования и суммирования. Так нечеткое множество, представленное ФП на рис. 1.2, можно записать в виде

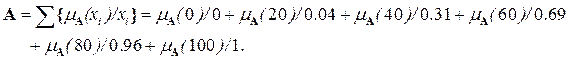
Из приведенных примеров мы видим, что конструкция нечеткого множества зависит от двух вещей: выбора подходящего универсума и выбора соответствующей функции принадлежности. Еще раз отметим, что выбор функции принадлежности является в сущности субъективным делом, из чего следует, что выбранные разными людьми функции принадлежности для одного и того же понятия (скажем, «холодный») могут значительно отличаться. Эта субъективность проистекает из неопределенной природы абстрактных понятий и не имеет ничего общего с вероятностью. Поэтому субъективность и неслучайность нечетких множеств являются главным отличием изучения нечетких множеств и теории вероятности. Последняя имеет дело с объективной трактовкой случайных событий (явлений).

Нормализация. Нечеткое множество называется нормализованным, если самое большое значение функции принадлежности, так называемая высота нечеткого множества, равно 1, Вы нормализуете нечеткое множество путем деления каждого элемента его функции принадлежности на упомянутое самое большое значение, a/max(a). При использовании функций принадлежности различают другие параметры, в частности ядро или сердцевину (см. рисунок ниже).

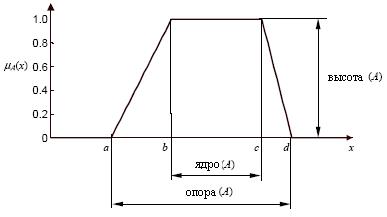
Ядро или сердцевина нормализованного нечеткого множества A включает все элементы x , для которых 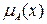=1. Четкое подмножество элементов, имеющих отличную от нуля степень принадлежности, называют основным (опорным) для нечеткого множества или носителем нечеткого множества. Опора или основа нечеткого множества A включает все элементы x , для которых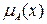 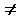0.