Набор логических операций

Фактически совокупность нечетких операций создает новое нечеткое множество из одного или нескольких заданных нечетких множеств (рис. 1.5).

Определение 1 (набор операций). Пусть A и B будут нечеткими множествами, заданными на одном и том же универсуме:

а) пересечение A и B (другими словами, T-норма) в большинстве случаев есть логическое произведение нечетких множеств A и B

.

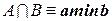Операция minесть операция по определению минимума для каждой пары соответствующих элементов векторов a и b. Здесь 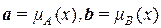представляют собой функции принадлежности множеств A и B соответственно.

Символ 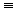означает, что новое множество имеет функцию принадлежности, определяемую частью выражения, расположенного справа от символа, т.е.

;

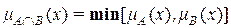б) объединение A и B (другими словами, S-норма или T-конорма) в большинстве случаев есть логическая сумма нечетких множеств A и B

,

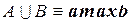где операция max есть операция по определению максимума для каждой пары соответствующих элементов векторов a и b;

в) дополнение A (другими словами, отрицание A) есть нечеткое множество

,

где каждое значение функции принадлежности множества A вычитается из 1.

Нечеткое множество A называется нечетким подмножеством множества B и обозначается как 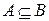, если значения его функции принадлежности для всех точек универсума меньше или равны значениям функции принадлежности B,

.

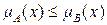Заде дал более наглядное и красивое определение операции пересечения как самого малого нечеткого множества, содержащего как A, так и B. Другими словами, если D есть нечеткое множество, содержащее как A, так и B, оно также содержит 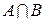. Объединение нечетких множеств может быть определено аналогично. Очевидно, что объединение A и B есть самое большое множество, которое содержит как A, так и B.

На рис. 1.5 показаны три простых операции над нечеткими множествами, причем, как видно, .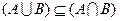

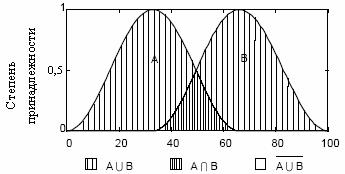
Рис. 1.5

Таблица 1

Коммутативность

Коммутативность

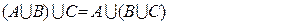Ассоциативность

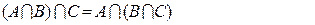Ассоциативность

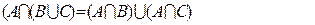Дистрибутивность

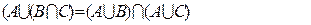Дистрибутивность 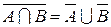Формула де Моргана

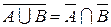Формула де Моргана

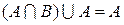Абсорбция

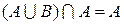Абсорбция

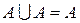Идемпотентность

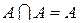Идемпотентность

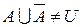Комплeментарность (дополнение) НЕудовлетворяется

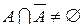Комплементарность (дополнение) НЕудовлетворяется

Пример 1.7 (покупка дома). Рассмотрим задачу принятия решения в условиях неопределенности, Пусть семья из четырех человек хочет купить дом. Как показатель комфортабельности они принимают число отдельных спален в доме. Однако, кроме того, они желают, чтобы сам дом был большим с точки зрения метража. Пусть u = [1 2 3 4 5 6 7 8 9 10] - множество доступных для покупки домов, описываемых числом имеющихся в них спальных комнат. Тогда нечеткое множество C (комфортабельный) можно описать как

.

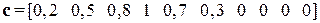Пусть нечеткое множество D (большой) определяется (для продаваемых домов) как

.

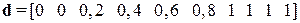При этом пересечение множеств комфортабельный и большой ( 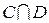) описывается функцией принадлежности

.

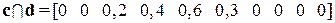Полученный результат можно интерпретировать так: 5 спален − наилучшее решение, но со степенью принадлежности 0,6; вторым с точки зрения пересечения будет решение 4 спальни.

Объединение множеств комфортабельный и большой ( 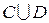)имеет функцию принадлежности

.

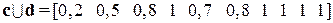Здесь 4 спальни является полностью удовлетворительным решением с точки зрения комфортабельности (степень принадлежности равна 1), а также дома с числом спален от 7 до 10, потому что эти дома очень большие. Кстати дополнение множества большой 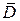описывается функцией принадлежности

.

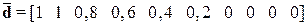Операци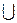и и 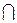ассоциативны, коммутативны и обладают еще другими свойствами (см. табл. 1). Эти свойства весьма важны, т.к. они помогают предсказать результат пространных рассуждений. Можно определить другие элементарные операции над множествами, однако обычно используются 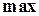и min.

Из последних двух свойств нечетких множеств следует: а) в отличие от логического произведения обычных (четких) множеств логическое произведение множества и его отрицания не обязательно образует пустое множество; б) точно так же логическая сумма нечеткого множества и его отрицания не образует универсальное множество. Заметим, что для четких множеств , .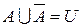

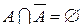Алгебраические бинарные операции над нечеткими множествами. Операции min и max вызывают некоторые трудности при анализе систем нечеткого логического вывода. Поэтому для вычисления T-норм и S- норм наряду с логическими используют алгебраические операции над нечеткими множествами.

Алгебраическое произведение нечетких множеств A и B (T-норма) обозначается A*B или 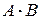и формулируется следующим образом

.

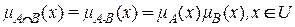Алгебраическая сумма этих множеств(S-норма) обозначается A+B и формулируется следующим образом

.

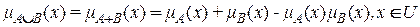Демонстрационные примеры, касающиеся операций над нечеткими множествами, можно найти в файлах MATLAB6p5\work\Fuzzy_Bab\krm05-2\example 1.m и example 2.m.

Модификаторы

Лингвистический модификатор является оператором, который возводит в степень нечеткое множество, другими словами, изменяет значение терма.

Например, в предложении «очень близко к нулю» слово очень модифицирует терм близко к нулю, который является нечетким множеством. Таким образом, модификация является унарной операцией над нечетким множеством. Примерами других модификаторов могут служить «немного», «более или менее», «возможно», «точно».

Даже несмотря на трудность ответа на вопрос, каков эффект от применения модификатора очень, по-видимому, ясно, что он усиливает эффект. Модификатор более или менее имеет противоположный эффект. Эти операторы

часто аппроксимируют следующими операторами

очень 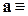a², более или менее 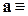a^1/2.

Унарная операция возведения в степень применяется к каждому элементу вектора 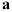поочередно. Здесь мы ограничились лишь возведением в квадрат и извлечением корня квадратного, но можно использовать любые другие показатели степени. Пусть имеем универсум в дискретной форме:

u = [0 20 40 60 80].

Тогдаисходя из функции принадлежности

множества молодой,можно получить дискретную функцию принадлежности для дискретного множества очень молодой путем возведения в квадрат всех элементов функции принадлежности множества молодой,

молодой ² = [1 0,36 0,01 0 0] .

Это символическая форма записи. На самом деле мы возводим в степень не само множество молодой, а соответствующую ему функцию принадлежности.

Функция принадлежности множества очень очень молодой определяется по индукции как

молодой ⁴ = [1 0,13 0 0 0].

Полученные множества наследуют универсум первичного множества. Кривые на рис. 1.3 были построены с использованием описанных здесь аппроксимаций.

Некоторые примеры других модификаторов имеют следующий вид

в высшей степени 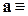a³

слегка 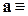a^1/3

до некоторой степени 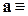более или менее a и не еле-еле a.

Все семейство модификаторов можно построить с помощью a^p, где - любая степень в пределах от 0 до бесконечности. При 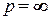модификатор можно назвать точно, потому что он подавляет (уничтожает) все значения функции принадлежности меньшие, чем 1.