Инференция (Нечеткий логический вывод)

Нечеткий логический вывод (также называемый как нечеткое или приближенное рассуждение) – это наиболее важный метод в нечеткой логике. Чтобы сделать заключение (вывод) из базовых правил, нам нужен механизм, который позволяет находить заключение из набора правил если-то. Такой механизм можно получить, используя композиционное правило нечеткого логического вывода (КПЛВ), другими словами, композиционное правило инференции, которое является существенным логическим обоснованием приближенных рассуждений. Инференция означает: сделать вывод из очевидного, сделать заключение или получить логическое следствие. Не путайте инференцию с интерференцией.

Чтобы понять лежащую в основе инференции концепцию, полезно рассмотреть вычисление значения четкой функции y=f(x), 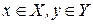(рис. 1.5), где f есть данная функция (определяет отношение между x и y), x есть независимая переменная (четкий аргумент), y – четкий результат. Если мы имеем x=a, то из y=f(x) делаем вывод, что значение y=b= f(a).

Последовательность действий.

Предпосылка 1 (факт или наблюдение): x = a,

Предпосылка 2: y=f(x) − отношение R=X 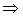Y (знание)

------------------------------------------------------------

Следствие: y=b=f(a)

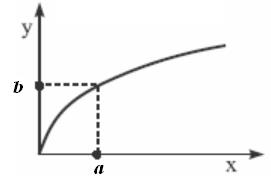
Рис. 1.5

Знаменитое правило инференции modus ponens (модус поненс) четкой логики (композиционное правило инференции)

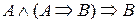, (1.14)

записываемое также как

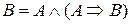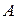
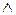= R, (1.14a)

может быть сформулировано следующим образом: если известно, что утверждение (высказывание) 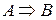верно (истина), и также, что А верно (истина), то можно сделать вывод, что B есть истина. Например, если А отождествляется с «помидор красный» и B с «помидор зрелый», то, если «помидор красный» есть истина, то также является истиной, что «помидор зрелый». Эта концепция иллюстрируется ниже

Предпосылка 1 (факт или наблюдение): x есть A,

Предпосылка 2 (правило) если x есть A , то y есть B ,

……………………………………………………………………………………

Следствие (заключение): y есть B.

Однако в большинстве человеческих рассуждений модус поненс используется приближенным образом. Например, если мы имеем то же самое правило импликации «если помидор красный, то помидор зрелый», и мы видим, что «помидор более или менее красный», то мы делаем вывод, что «помидор более или менее зрелый». Эту последовательность действий можно записать как

Предпосылка 1 (факт или наблюдение): x есть A^’,

Предпосылка 2 (правило) если x есть A ,то y есть B ,

……………………………………………………………………………………

Следствие (заключение): y есть B^’.

Здесь A^’ близко к A и B^’ близко к B. Когда A, B, A^’ и B^’ являются нечеткими множествами соответствующих универсумов, то описанная выше процедура инференции называется нечетким рассуждением или приближенным рассуждением; также ее называют обобщенным правилом modus ponens (ОМП), т.к. в частном случае оно преобразуется в модус поненс.

Используя композиционное правило инференции, сформулированное ранее, мы можем сформулировать процедуру нечеткой инференции как следующее определение.

Определение: Нечеткий логический вывод.

Пусть A, A^’ и B представляют собой нечеткие множества на универсумах U, U и V соответственно. Предположим, что нечеткая импликация 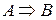выражена как нечеткое отношение R на 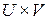. Тогда нечеткое множество B^’ , логически выводимое из «x есть A^’ » и нечеткого правила «если x есть A ,то y есть B» определяется как

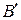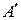
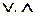
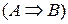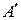
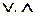= = R. (1.15)

Часто для непрерывных универсумов используют вместо обозначения оператора композиции 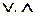( внутреннего произведения) другое обозначение :

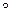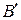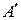
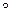
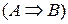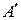
= = R.

При этом в нечеткой логике 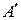и 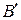слегка отличаются в некотором смысле от 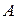и 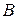соответственно, например, после применения модификаторов.

ОМП тесно связано с ранее рассмотренным прямым построением цепочки (см. п.1.3), т.е. рассуждениями от исходных посылок к целевой гипотезе в базовых правилах, которые содержат цепочки правил. Такая связь особенно полезна в нечетких контроллерах. ОМП имеет в своей основе композиционное правило инференции. При этом связь лингвистических переменных 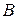и 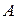, т.е. выражение (1.14а), называют лингвистической (словесной) моделью, представленной с помощью отношения R (рис. 1.5,а).

Применительно к базовым правилам правило модус поненс выглядит так:

Пример. Уровень жидкости в баке

Классическая логика

Предпосылка 1(факт): уровень есть НИЗКИЙ

Предпосылка 2: если уровень (x) есть НИЗКИЙ (A), то входной сигнал V₁ (y) вентиля есть ОТКРЫТЬ (B)

………………………………………………………………………………………

Следствие: входной сигнал V₁ вентиля есть ОТКРЫТЬ

Нечеткая логика

Предпосылка 1(факт): уровень есть НЕ ОЧЕНЬ НИЗКИЙ ( )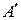

Предпосылка 2: если уровень есть НИЗКИЙ, то входной сигнал V₁ вентиля есть ОТКРЫТЬ

------------------------------------------------------------------------

Следствие: входной сигнал V₁ вентиля есть НЕМНОГО ОТКРЫТЬ ( )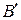

Таким образом, процесс получения нечеткого логического вывода 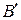с использованием данных наблюдения (измерения) 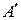и знания Rсводится ккомпозиции 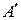и R, т.е.

.

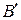
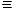
Пример 1.14 (ОМП). Рассмотрим нечеткое отношение

R=низкий 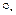min открыть

из предыдущего примера, и вход контроллера (фактическое измерение уровня), представляющий собой нечеткое множество НЕ ОЧЕНЬ НИЗКИЙ уровень с дискретной функцией принадлежности

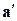= не очень низкий = [0,75 1 0,75 0,5 0,25]

тогда, чтобы получить нечеткий логический вывод, найдем композицию нечеткого множества 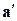и отношенияR (внутреннее произведение):

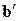= v₁ =не очень низкий 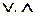R (1.16)

Очевидно, что фактический вход «НЕ ОЧЕНЬ НИЗКИЙ уровень», представляет уровень несколько более высокий, чем «НИЗКИЙ». В результате после инференции получаем выход как нечеткое множество V₁ «НЕМНОГО ОТКРЫТЬ ВЕНТИЛЬ» чуть меньший, чем «ОТКРЫТЬ».

В нечеткой лингвистической модели (в нечетком правиле для примера 1.13) вход – лингвистическая переменная уровень, выход – лингвистическая переменная входной сигнал вентиля.

Между прочим, если мы попытаемся приравнять в (1.16) функции принадлежности предполагаемого входа низкий и фактического входа не очень низкий, то следует ожидать получить после композиции с R функцию принадлежности выхода как вектор v₁, равный вектору открыть. Да, это действительно так. Однако доказательство оставим как упражнение для студентов.

Можно показать, что композиция множества 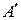и отношения R

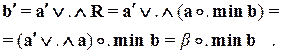(1.19)

Здесь a, b, 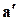, 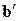соответственно функции принадлежности множеств A, B, , ,

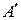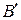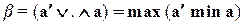. (1.20)

Для примеров 13 и 14 с помощью (1.19) и (1.20) получаем

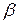= max{[0,75 1 0,75 0,5 0,25] min[1 0,75 0,5 0,25 0]}

=max{0,75 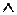1; 1 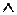0,75; 0,75 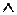0,5; 0,5 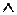0,25; 0,25 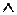0}=0,75.

Следовательно,

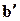=0.75 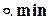b =[0,75 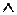0; 0,75 0,5; 0,75 1]=[0 0,5 0.75],

что совпадает с (1.18).