Логические связки (соединения)

В ежедневных разговорах и в логике фразы (высказывания) связывают с помощью слов не, и, или, если - то (или импликация) и если и только если. Эти слова называют связками. Высказывание, которое модифицируется с помощью слова «не», называется отрицанием исходного высказывания. Слово «и» используется, чтобы объединить два высказывания в форме конъюнкции (от conjunction - союз, связь) двух высказываний. Аналогично высказывание, которое образовано путем соединения двух высказываний с помощью слова «или», называется дизъюнкцией (от disjunction − разобщение) двух высказываний. Из двух высказываний мы можем построить некое высказывание с помощью формы «Если…то…»; последнее называют условным высказыванием (предложением). Высказывание, стоящее за словом «Если», называется антецедентом (предпосылкой), а высказывание, следующее за словом «то», называют консеквентом (следствием) или заключением. Таким образом, антецендент является первой частью условного высказывания (предложения), а консеквент – второй частью этого условного высказывания. Другие идиомы (словосочетания), которые мы будем считать, имеющими то же самое значение (тот же самый смысл), что «если p, то q» (где p и q есть высказывания), звучат как «p влечет за собой q», «p только, если q»,

«q, если p» и т.п. Слова «если и только если» (или эквивалентность) используются, чтобы из двух высказываний образовать двухусловное высказывание, которое принимает значение истина в случае истинности обоих высказываний одновременно и значение ложь в остальных случаях. Надо сказать, что операция, называемая импликацией высказываний (от implico – тесно связываю), в общем случае отличается от базового правила (правила продукции) Если A, то B. Действительно, логическая импликация высказываний не заключает в себе никакой причины, никакой временной или иной взаимосвязи между предпосылкой и следствием.

Путем введения букв и специальных символов структура связок может быть показана красноречивым образом. Наш выбор символов имеет такой вид

для «не»

для «и»

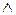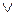для «или»

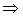для «если-то»

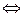для «если и только если»

В нечеткой логике расширения «не», «и» и «или» также называют нечетким отрицанием, T-нормой и S-нормой соответственно.

Импликация

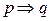
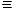
Оператор импликация на протяжении длительного времени не дает покоя теоретикам нечеткой логики. Если мы его определим классическим (традиционным) путем, т.е. как , то мы получим таблицу истинности, которая противоречит интуиции и непригодна, т.к. некоторые законы логики ею не поддерживаются, теряют силу. Под таблицей истинности понимают таблицу, определяющую истинность результата рассматриваемой операции для каждого из значений истинности исходного или исходных высказываний. Кстати, к законам логики относятся, например, закон противоречия, закон двойного отрицания, закон доказательства от противного и другие.

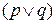
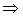
Многие ученые пытались дать иные определения импликации. В литературе, например, приводится список из 72 ее альтернативных определений. Одним из таких определений является так называемая импликация Гёделя, которая лучше в смысле того, что многие из «прежних, достаточно старых» (читай двухзначных) логических отношений при ее использовании имеют силу. Тремя другими примерами являются: 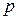(упрощение или симплификация), 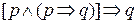(правило отделения или modus ponens (модус поненс)) и 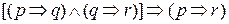(гипотетический силлогизм). Импликация Гёделя может быть записана так

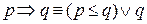, (1.9)

где

.

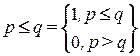Правило Если уровень в баке есть НИЗКИЙ, то входной сигнал V₁ вентиля есть ОТКРЫТЬ является импликацией, т.к. переменная уровень влечет за собой значение V₁ на выходе регулятора. Однако импликация Гёделя,

редко используется в нечетких регуляторах (контроллерах). Значительно чаще применяется импликация, называемая импликацией Мамдани.

Определение (импликация Мамдани). Пусть A и B два нечетких множества, не обязательно заданные на одном и том же универсуме, определяемые своими дискретными функциями принадлежности a и b соответственно. Импликация Мамдани определяется как

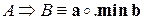, (1.12)

где 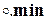есть внешнее произведение, применяющее операцию min к каждому элементу декартова произведения a и b.

В отличие от классической импликации, которая говорит о том, что «A влечет за собой B», но ничего нельзя сказать о B, когда A не имеет место ( A и B нельзя менять местами), импликация Мамдани трактует правило Если A, то B как «Истина, что A и B одновременно имеют место». Последняя импликация симметрична и может быть инвертируема и записывается в ряде случаев как конъюнкция A и B, т.е. как A 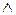B .

Пусть aпредставляет собой вектор-столбец и b вектор-строку, тогда их

внешнееmin- произведение может быть найдено в виде «таблицы умножения».

(1.13)
Здесь a_i = 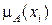и b _j = 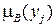соответственно элементы дискретных функций принадлежности a и b множеств A и B.

Таким образом, импликация Мамдани представляет собой нечеткое отношение множеств A и B и определяется по формуле

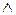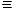R =A B a 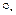min b.

Матрицу Rможно записать в виде R=[r _ij], где r _ij 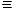a_i 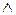b _j – (i,j)-й элемент матрицы R.

Для непрерывных универсумов нечеткое отношение имеет следующий вид

.

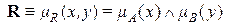Как видим, каждое правило можно трактовать как импликацию, другими словами, как нечеткое отношение.

Пример 1.13 (внешнее произведение). Рассмотрим импликацию (правило) «Если уровень есть НИЗКИЙ, то входной сигнал V₁ вентиля ОТКРЫТЬ»с переменными (нечеткими множествами) НИЗКИЙ(A) и ОТКРЫТЬ(B), определяемыми c помощью дискретных функций принадлежности как

a= низкий = [ 1 0,75 0,5 0,25 0]

b=открыть = [0 0,5 1].

Тогда импликация,рассматриваемая как нечеткое отношение множествНИЗКИЙи ОТКРЫТЬ, т.е. какR=низкий 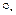min открыть,в соответствии с (1.13)

вычисляется по следующей схеме

(1.13а)

Это есть весьма важный путь построения таблицы импликации исходя из правил.

Здесь a= ,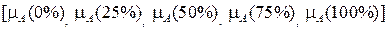

b= .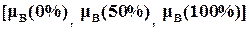

Внешнее min - произведение Мамдани так же, как и внешнее произведение с операцией 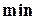, заменяемой операцией * для произведения, есть основа для построения большинства нечетких контроллеров; поэтому в последующем мы будем часто его использовать. Однако следует отметить, что Задэ и другие ученые предложили несколько других теоретических определений импликации.

Заметим, что импликация 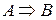рассматривается как база знаний или просто как знание.

Лекция 5