Динамика электронов в кристалле

Поскольку импульс электрона 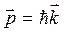, соотношение неопределенностей можно записать в виде:

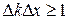(39.5)

Отсюда вытекает, что при точном определении k положение электрона в кристалле ( 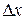) будет совершенно неопределенным. О скорости же электрона в кристалле можно говорить только если он хотя бы приближенно локализован в пространстве.

Пусть ∆k ≠ 0. Тогда электрон будет локализован в пределах области с размерами порядка

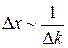(39.6)

Согласно принципу суперпозиции состояний волновая функция электрона может быть представлена в виде суммы плоских волн вида 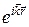, значение волновых чисел заключены в пределах ∆k. Если ∆k невелико, то суперпозиция плоских волн образует волновой пакет. (Напомним: волновой пакет есть результат наложения плоских волн, волновые числа которых заключены в малом интервале.) Как мы знаем, максимум амплитуды результирующей волны, возникающей при наложении составляющих пакета, перемещается со скоростью

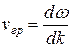, (39.7)

которую называют групповой скоростью. Наиболее вероятное местонахождение электрона совпадает с центром группы волн. Поэтому 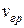есть скорость электрона в кристалле.

Поскольку

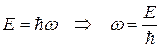, (39.9)

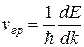, (39.10)

Пусть теперь к кристаллу приложено внешнее поле с напряженностью 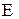. На электрон в кристалле действуют две силы:

· сила периодического поля решетки F_крист и

· электрическая сила .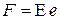

За время dt сила F совершит работу 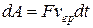. Или, с учетом (39.10),

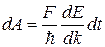. (39.11)

Эта работа идет на приращение энергии электрона в кристалле: dA = dE. Поэтому

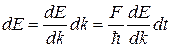. (39.12)

Отсюда следует важное соотношение:

. (39.13)

Ускорение электрона в кристалле

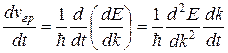. (39.14)

Подставив в (39.14) отношение (39.13), получим:

. (39.15)

Преобразуем (39.15) к виду, т.е. выразим силу, действующую со стороны электрического поля: т.е. ние ое соотношение

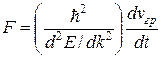. (39.15)

Из (39.15) вытекает, что ускорение электрона в кристалле пропорционально силе, действующей со стороны электрического поля F. Это не является очевидным результатом, поскольку на электроны в кристалле действует силаF_крист. Все было бы как в законе Ньютона, если бы ускорение было пропорционально сумме сил!

Уравнение (39.15) можно записать в виде:

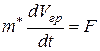. (39.15)

где называется эффективной массой электрона в кристалле. 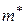может сильно отличаться от массы электрона m_e, например принимать отрицательные значения. Это связано с тем, что 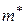неявно учитывает действие силы F_крист. Однако, приписав электрону массу 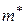можно рассматривать его движение под действием поля 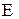, считая электрон свободным. Таким образом, соотношения, полученные для свободных электронов, остаются справедливыми и для электрона в кристалле, но имеющего .

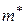Эффективная масса зависит от местоположения электрона внутри разрешенной энергетической зоны.

Вблизи дна энергетической зоны – точки типа 1, зависимость Е (k) примерно такая же как и для свободных электронов. Поэтому в таких точках m @ m^*.

Точки типа 2 являются точками перегиба на зависимости Е(k). В таких точках перегиба 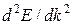= 0. Соответственно m^* ® ¥. Реально это означает, что внешнее поле не может оказать влияния на электрон, состояние которого соответствует точке 2. (Не забывайте, что действует еще и F_крист.)

Вблизи потолка разрешенной зоны (в точках типа 3) < 0. Поэтому m* < 0. Это означает, что под действием 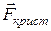, и электрон ускоряется в сторону, противоположную внешней электрической силе.