Собственная проводимость полупроводников.

<79 80 81 82 838485 >

Напомним, что полупроводники – это кристаллы, которые при низких температурах имеют полностью заполненную валентную зону. (Название зоны отражает тот факт, что в модели сильно связанных полупроводников эта зона возникает при расщеплении энергетического уровня, на котором в отдельных атомах находились валентные электроны.) Поэтому при низких температурах полупроводники являются изоляторами. В отличие от классических диэлектриков у полупроводников полностью заполненная валентная зона отделена от следующей зоны разрешенных значений энергии запрещенной зоной шириной порядка одного электрон-вольта. В диэлектриках этот параметр составляет порядка 3 эВ. Не очень большая ширина запрещенной зоны обеспечивает возможность осуществления в полупроводниках явления, отличающего их от классических диэлектриков: с ростом температуры и возрастанием интенсивности теплового движения становится возможным получение отдельным электроном энергии, достаточной для перехода в зону разрешенных энергий. (Принципиально этот процесс возможен и в диэлектриках, однако температуры необходимые для этого столь высоки, что не совместимы с существованием кристалла.)

Попав в свободную зону, электроны не могут сразу вернуться в валентную зону, поскольку в окружающем пространстве состояния с соответствующей энергией заняты. Если к кристаллу приложить внешнее электрическое поле, электроны будут получать от него энергию, ускоряться в направлении против вектора его напряженности и переносить заряд, т.е. создавать электрический ток. Поэтому в полупроводниках (!) свободную зону разрешенных значений энергии, ближайшую к валентной называют зоной проводимости.

При переходе электрона в зону проводимости в валентной зоне освобождаются энергетические уровни вблизи ее потолка. Электроны валентной зоны получают возможность ускоряться в электрическом поле, увеличивая свою энергию и занимая освободившиеся уровни. Однако эффективная масса электронов вблизи потолка валентной зоны отрицательна, и движение таких электронов удобнее рассматривать как движение дырок. Причем количество дырок в валентной зоне совпадает с количеством электронов в зоне проводимости. Проводимость полупроводника в условиях, когда носители заряда образуются только за счет термических забросов электронов валентной зоны в зону проводимости, называется собственной. Такой проводимостью обладают химически чистые полупроводники. Процесс возникновения свободного электрона в зоне проводимости и дырки в валентной называют генерацией электронно-дырочной пары.

Распределение электронов по уровням, описывается функций распределения: . График этой функции при температурах, когда собственная проводимость стала существенной приблизительно показан на рисунке 41.1.

Расчеты показывают, что если отчитывать от потолка валентной зоны, то положение уровня Ферми в собственном полупроводнике описывается выражением:

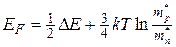(41.4)

где и 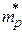- эффективные массы электронов и дырок,

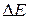- ширина запрещенной зоны.

Обычно эффективные массы электронов и дырок отличаются незначительно, и вторым слагаемым в (41.4) можно пренебречь по сравнению с . Поэтому с высокой точностью можно утверждать, что в собственных полупроводниках уровень Ферми находится в середине запрещенной зоны:

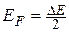. (41.5)

Для электронов в зоне проводимости справедливо соотношение:

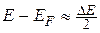и , . (41.6)

В этом случае вместо распределения Ферми-Дирака можно использовать распределение Больцмана, в соответствии с которым вероятность заполнения энергетического уровня с энергией 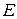равна:

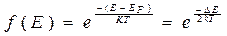. (41.7)

Количество электронов в зоне проводимости, а значит и их концентрация, пропорционально этой вероятности. Поскольку проводимость 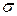, в свою очередь, пропорциональна концентрации электронов, то температурная зависимость проводимости описывается выражением:

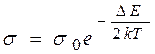. (41.8)

Логарифмируя это выражение, получаем:

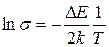. (41.8)

Таким образом, температурная зависимость электропроводности полупроводника с собственной проводимостью в координатах 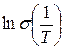должна иметь вид прямой линии, наклон которой определяется шириной запрещенной зоны, как это показано на рисунке 41.2. Экспериментальные исследования подтвердили справедливость выводов зонной теории электропроводности.

Очень часто при рассмотрении проводимости полупроводников полезными оказываются модельные представления. Для типичных полупроводников 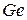и кристаллическую структуру можно представить на плоскости в виде, показанном на рисунке 41.3. Каждый атом обладает четырьмя валентными электронами, которые образуют связи с четырьмя ближайшими атомами. При достаточно высокой температуре происходит разрыв некоторых связей. Освободившийся электрон оказывается в межузельном пространстве и может участвовать в создании электрического тока, а в окрестности разорванной связи появляется нескомпенсированный положительный заряд. Валентные электроны данного атома могут восстановить связь в месте ее разрыва, однако при этом разорванная связь сместится в другое место. Если разорванная связь за счет перехода электронов от других атомов будет перемещаться по кристаллу, то вместе с ней будет перемещаться и положительный заряд, который можно считать моделью дырки.

При достаточно высокой концентрации свободных электронов и дырок может происходить захват свободного электрона атомом для заполнения разорванной связи. При этом исчезают электрон и дырка. Такой процесс называется рекомбинацией электронно-дырочной пары. В представлениях зонной теории рекомбинации соответствует переход электрона из зоны проводимости в валентную, сопровождающийся выделением энергии, которая может быть унесена фотоном или передана кристаллической решетке.

<79 80 81 82 838485 >

Дата добавления: 2021-01-11; просмотров: 248;