Условие устойчивости сжатого стержня.
Устойчивость сжатого стержня считается обеспеченной, если допускаемая сжимающая сила равна:
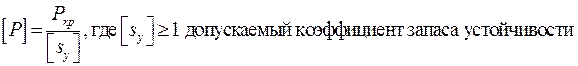
Под устойчивым прямолинейным равновесием понимается состояние, при котором стержень возвращает свою прямолинейную форму после прекращения действия продольной сжимающей силы.
Неустойчивое прямолинейное равновесие, при котором прямолинейная форма не возвращается после прекращения действия силы.
Критической силой называется такое её минимальное значение, при котором стержень из устойчивого равновесия переходит в неустойчивое.
Формула Эйлера справедлива для случая, когда напряжения, возникающие в стержнях, меньше предела пропорциональности:
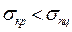
Если значение критической силы разделить на площадь сечения стержня, то получим значение критического напряжения:
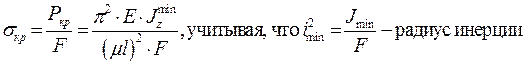
Получим:
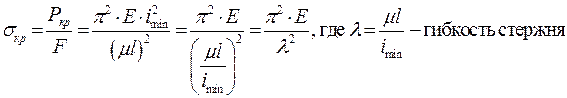
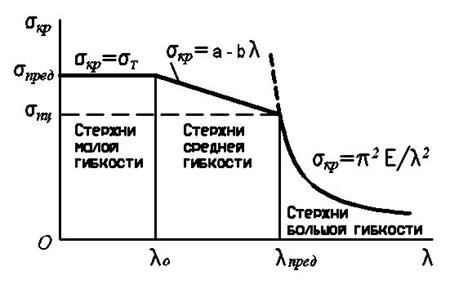
Гибкость стержня характеризует влияние размеров стержня и способа закрепления его концов и равна отношению приведённой длины стержня к радиусу инерции.
Чем больше гибкость, тем меньше критическое напряжение.
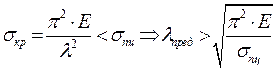 - значение предельной гибкости стержня – условие, при котором формула Эйлера применима.
- значение предельной гибкости стержня – условие, при котором формула Эйлера применима.
Когда формула Эйлера не применима, то пользуются формулой Ясинского:
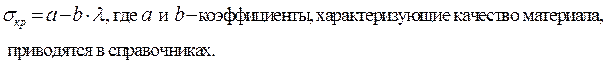
Задача №1: Проверить на устойчивость сжатую стойку, если
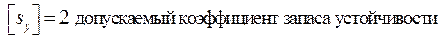 . Длина стойки
. Длина стойки
l =3 м, 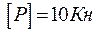 ,
, 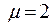 (Один конец защемлён, жёсткое закрепление, а другой свободен), в поперечном сечении стойки прямоугольник с размерами 40 мм и 80 мм.
(Один конец защемлён, жёсткое закрепление, а другой свободен), в поперечном сечении стойки прямоугольник с размерами 40 мм и 80 мм.
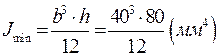
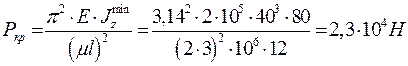
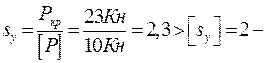 устойчивость обеспечена.
устойчивость обеспечена.
Задача№2: Рассчитать радиус инерции для круга:
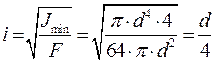
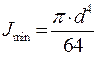
Задача№3: Рассчитать радиус инерции для прямоугольника:
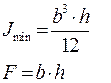
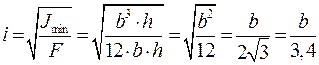
Дата добавления: 2021-01-11; просмотров: 610;











