Лекция №6 «Продольный изгиб. Формула Эйлера. Условие устойчивости сжатых стержней».

<5 678 9 10 11 >

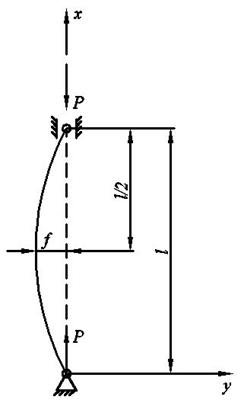
Нужно найти формулу зависимости 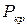- критической силы (минимальное значение сжимающей силы, при которой возможен продольный изгиб) от геометрических размеров стержня и механических характеристик материала. Данная формула была выведена знаменитым математиком и механиком Леонардом Эйлером в 1744г.

Определим изгибающий момент 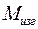методом сечений. Запишем условие равновесия для оставшейся части:

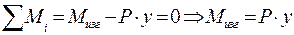- изгибающий момент в любом сечении стержня.

у – уравнение упругой линии стержня

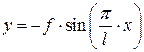- синусоида, знак «-», так как расположена ниже нулевой оси;

f – величина стрелы прогиба.

На концах стержня при х=0 и при х=l у=0 прогиба не будет.

Посередине стержня при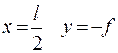

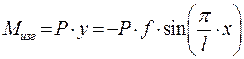
Подставим значение 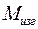в приближённое дифференциальное уравнение упругой линии:

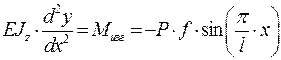
Проинтегрируем один раз, получим:

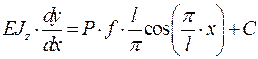
Найдём постоянную интегрирования из граничных условий при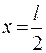

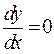, так как касательная к упругой линии в середине стержня параллельна оси ох. Следовательно С = 0.

Проинтегрируем во второй раз, получим:

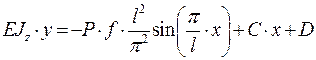
Найдём постоянную интегрирования D из условия: при при х=0 прогиб у=0, следовательно D=0.

Значит:

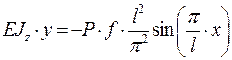
Так как при 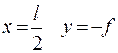, следовательно:

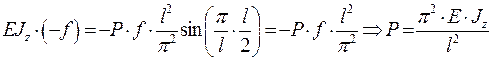
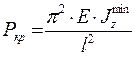- критическая сила для стержня с шарнирными опорами на концах (формула Эйлера).

l – длина стержня .

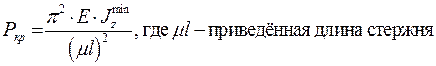
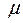- зависит от способа закрепления концов стержня и показывает во сколько раз следует изменить длину шарнирно закреплённого стержня, чтобы критическая сила для него была равна критической силе стержня в данных условиях закрепления.

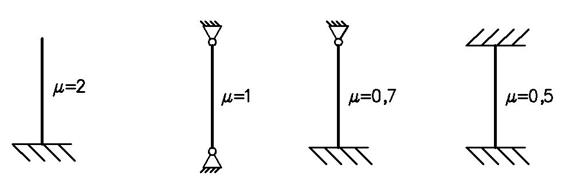
Значения 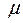для различных способов закрепления концов стержня.

Оба конца закреплены без шарниров (жёсткое закрепление) -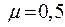

Один конец с шарнирно- закреплён, а другой конец защемлён -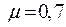

Оба конца шарнирно-закреплены -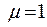

Один конец защемлён (жёсткое закрепление), а другой свободен –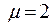

<5 678 9 10 11 >

Дата добавления: 2021-01-11; просмотров: 377;