Законы булевой алгебры.
Законы булевой алгебры можно выразить в виде формул:
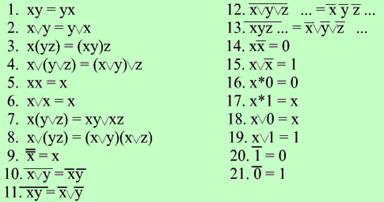
Удобно выделить законы, облегчающие преобразования формул к более простому виду, хотя они выводятся из ранее введенных.
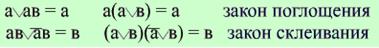
Логические выражения булевой алгебры (булевы выражения) задают булевы функции, т.к. для каждого набора значений переменных булевого выражения можно определить значение всего выражения. При этом значение булевого выражения может быть либо 0, либо 1, как и значения исходных переменных.
Функция называется булевой, если она определена на всех наборах значений двоичных переменных, от которых зависит функция.
Булеву функцию всегда можно задать таблицей.
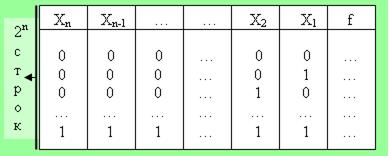
Для задания булевой функции необходимо знать множество наборов, при котором функция равна "1" – М1 (множество единичных наборов), либо множество наборов, на которых функция принимает значение "0" – множество М0.
Множество всех наборов значений n переменных обозначается "En".
Задав М1, известно, что М0 - это набор из En, не вошедший в М1 (и наоборот).
Выведем формулу для множества всех наборов значений n переменных. Пусть М1 - множество наборов, при котором функция равна "1", М0 - множество наборов, при котором функция равна "0", а En - множество всех наборов значений n переменных. Тогда Еn будет определяться как:
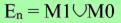
Наборы значений переменных булевых функций можно рассматривать как двоичные числа.
Например:
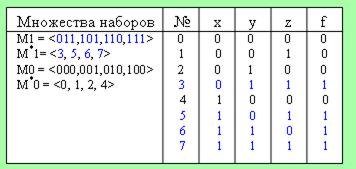
Часто вместо множества наборов значений аргументов булевых функций рассматриваются множества номеров наборов значений аргументов. При этом вместо М1 берется М*1 (как в примере с таблицей).
Функция может не зависеть существенно от некоторых переменных. По определению f (x1, x2, ... , x0, xn) не зависит существенно от xi, если на любом наборе переменных f (x1, x2, ... , 0, ... , xn) = f (x1, x2, ... , 1, ... , xn).
Пусть имеем две булевы переменные x и y. Количество различных сочетаний значений этих переменных равно 16. Соответственно для двух булевых переменных можно определить 16 булевых функций.
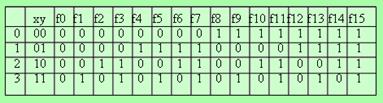
Ниже приведены названия этих булевых функций.
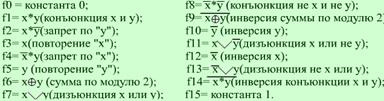
Дата добавления: 2016-09-26; просмотров: 3848;











