Основы автоматных преобразований

Цифровой (конечный) автомат – это образ элемента с конечной памятью, который реализуется через механизм «смены состояний», каждое из которых отражает некоторую предысторию поступления входных сигналов. В разных состояниях автомат может по-разному реагировать на одинаковые входные воздействия.

Под воздействием входного слова (последовательности символов, возникающей в моменты времени t = 0, 1, 2, ... i ... , которые называются тактами) автомат переходит из одного состояния в другое и выдает выходное слово. Слово на выходе автомата в такте определяется в общем случае входным словом, поступившим в этом такте на вход автомата, и внутренним состоянием автомата, которое явилось результатом воздействия на автомат входных слов в предыдущие такты. Таким образом восприняв сигнал Хt в ответ автомат формирует сигнал Yt с учетом предыстории.

При анализе автомата его заменяют автоматом с одним эквивалентным входом и одним эквивалентным выходом и считают, что эквивалентные входной сигнал Xt и выходной сигнал Yt принимают значения из соответствующих образом преобразованных алфавитов входных и выходных сигналов.

Рассмотрим примеры автоматов.

1.

Yt=1, если Xt=9, а непосредственно перед этим было Xt-1=2, Xt-2=1 и

Xt-3 = 1; в противном случае Yt = 0.

2.

Yt = 1, если Xt = 1 и до такта t число единичных значений Xi было нечетно; в противном случае Yt = 0.

Для автоматов существует формализованная система описания (автоматные преобразования).

Чтобы описать автомат нужно задать закон (функцию) переходов автомата из одного состояния в другое и функцию выходов (реакции на входные воздействия в каждом состоянии).

Опишем рассмотренный ранее автомат А2.

1) X=(0, 1) - входной алфавит.

2) Y=(0, 1) - выходной алфавит.

3) S=(S0, S1) - алфавит состояний. S0 - отражает факт прихода

ранее четного числа X=1. S1 - отражает факт прихода

ранее нечетного числа X=1.

4) S0 - начальное состояние автомата.

5)S(t)= Ф(X(t), S(t-1)) - функция переходов;

Y(t)= F(X(t), S(t-1)) - функция выходов.

Функция переходов и функция выходов однозначно определяют зависимость состояния автомата в такте t и зависимость выходного сигнала Y(t) от входного сигнала в такте t и состояния в такте (t-1).

Пример табличного описания автомата А2:

функции переходов. функции выходов.

Посмотрим, как по такому описанию можно проанализировать поведение автомата А2 в моменты времени t = 0, 1, 2, 3, 4. Пусть задано начальное состояние автомата S0 и значение входных сигналов в указанные моменты времени:

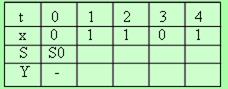
Найдем последовательность Y и S:

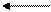Y(t)=F(X(t), S(t-1));

S(t)=Ф(X(t), S(t-1)).

Алгоритм заполнения таблицы:

1. Зная S(t-1) и X(t), определяем Y(t) по функции выходов.

2. Зная S(t-1) и X(t), определяем S(t) по функции переходов.

3. Возвращаемся к пункту 1.

Получим следующую последовательность Y(t) и S(t).

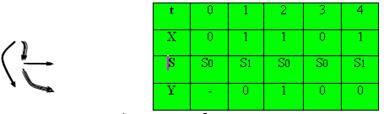
Автомат может быть описан и в виде ориентированного графа. При этом состояния автомата представляются вершинами графа, входы и выходы автомата отмечаются соответственно как числители и знаменатели дробей, расположенных на дугах, направленно соединяющих вершины графа.

Ниже приведено графическое задание автомата А2.

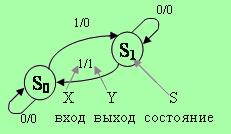
Функциям вида:

Y(t)=F(X(t),S(t-1)),

S(t)=Ф(X(t),S(t-1)), t=1,2, ...

соответствует автомат, выходной сигнал которого зависит от состояния автомата и сигнала на его входе. Такой автомат называется автоматом МИЛИ.

Рассмотрим автомат МИЛИ как устройство, работающее в некоторой системе тактов (часов). Его поведение можно описать следующей блок-схемой:

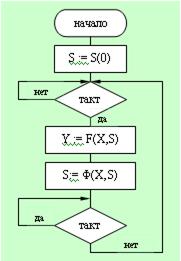
Выход автомата МИЛИ в такте t зависит от воздействия в такте t:

Y(t)=F(X(t),S(t-1))

В устройствах ЭВМ также широко применяются и так называемые автоматы с задержанной реакцией. У таких автоматов выходной сигнал Y(t) в такте t зависит исключительно от состояния автомата S(t-1) в такте и не зависит от входного сигнала X(t). Наиболее изученные и употребляемые автоматы такого вида это - автоматы МУРА.

Функционирование автомата МУРА описывается выражениями:

S(t)=Ф(X(t), S(t-1)),

Y(t)=F(S(t-1)), t=1,2, ...

Пример графического описания некоторого автомата МУРА:

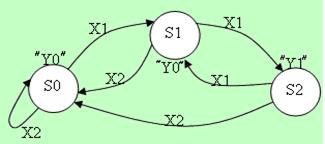
Выходы "Y" определяется только значением состояний S и соответственно задается не на дугах, а у вершин. Входы, как и в автомате Мили, задаются на дугах.

Функции переходов и выходов для автоматов МУРА также могут задаваться в форме таблиц.

Пусть задано графическое описание автомата Мура:

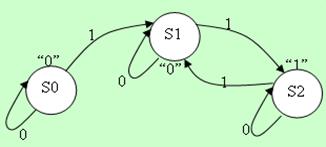
X =<0;1>

Y = <0;1>

Соответствующее табличное описание имеет вид:

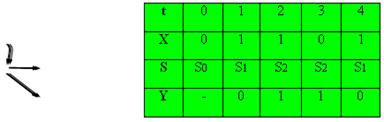
Поведение описанного автомата Мура во времени отражает приведённая ниже таблица.

Литература.

1. Бройдо В. Л. Вычислительные системы, сети и телекоммуникации.

Учебник для вузов, СПб., "Питер", 2003.

2. Букчин Л., Безрукий Ю., Дисковая подсистема IBM-

совместимых персональных компьютеров, //М., МП "Бином", 1993

3. Воробьев М. Серверы IBM. Статья., MVorobyev@hetnet.ru

4. Гук М. Ю. Аппаратные средства ПК. Энциклопедия,

СПб, "Питер", 2003

5. Дейт, К., Дж. Введение в системы баз данных. 7-е издание:

пер. с англ., М., "Вильямс", 2001.

6. Каган Б.М. Электронные вычислительные машины и системы,

М., "Энергоатомиздат", 1991.

7. Комер Д. Принципы функционирования Интернета:

пер. с англ., СПб., "Питер", 2002.

8. Мюллер, Скотт. Модернизация и ремонт ПК. 13-е издание.:

пер. с англ., М., "Вильямс", 2002.

9. Олифер В. Г., Олифер Н. А. Компьютерные сети. Принципы,

технологии, протоколы. Учебник для вузов, СПб., "Питер", 2003.

10. Петров М. Н., Молочков В.П. Компьютерная графика,. Учебник для вузов, СПб., "Питер", 2002.

11. Пржиялковский В., Ломов Ю., "Технические и программные

средства единой системы ЭВМ", //М.,Статистика, 1980

12. Рейнбоу В. Компьютерная графика. Энциклопедия:

пер. с англ., СПб., "Питер", 2003.

13. Симонович С. В. Информатика. Базовый курс. 2-е издание,

СПб., "Питер", 2005.

14. Таненбаум Э. Архитектура компьютера: пер. с англ.,

СПб., "Питер", 2003.

15. Таненбаум Э. Компьютерные сети: пер. с англ.,

СПб., "Питер", 2003.

16. Таненбаум Э. Современные операционные системы.

2-е издание, СПб., "Питер", 2002.

17. Хамахер К., Вранешич З., Заки С. Организация ЭВМ:

пер. с англ., СПб., "Питер", 2003.

18. Шамров М.И. Шаруненко Н.М. Высокопроизводительные вычислительные системы на железнодорожном транспорте – Учебное пособие, МИИТ, 2006

19. Олифер В.Г., Олифер Н.А. Компьютерные сети. СПб., "Питер", 2005

20. Ресурсы интернета:

www. peoples.ru/ scien

www. computer - museum.ru

www. citforum.ru/hardware/svk/glava_2.shtml#Мейнфреймы

www. IBM.com.