Происхождение уравнений кригинга

Задача состоит в следующем: мы имеем N значений данных z(x₁), …, z(x_N) в нашем районе, и мы хотим оценить линейную функцию переменной Z(x). Например, мы можем захотеть оценить ее значение в конкретной точке Z(x₀), или ее среднее по определенному региону. (Некоторые другие линейные функционалы, такие как градиент, также могут быть оценены с помощью кригинга.) Чтобы избежать необходимости описания всех случаев раздельно, мы обозначим оцениваемое множество через:

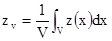[7.1]

Объем V может быть всем месторождением, или добываемым блоком, или он может быть таким маленьким, как одна точка, в случае точечной оценки. Он может быть даже неправильной формы. Для большей информации по кригингу объемов неправильной формы смотрите Рамку 5. Чтобы оценить Z(V), мы запишем взвешенное среднее данных:

[7.2]

где l_i – факторы взвешивания. По договоренности звездочка будет использоваться для обозначения оценки значения, как противопоставление действительному, но неизвестному значению. Проблема заключается в определении лучшего способа выбора факторов взвешивания. Т.е. найти область, где мы можем использовать геостатистическую модель. Мы предполагаем пространственную переменную:

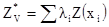[7.3]

Веса выбираются такие, чтобы оценка была:

несмещенной: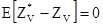

с минимальной дисперсией: 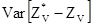- минимально.

Эту дисперсию мы будем называть дисперсией кригинга.