Изменение основания: регуляризация

Обозначим за Z(x) случайную функцию, определенную на точечном основании. Ее среднее для объемов V определяет новую случайную функцию Z_v (x) с основанием V. Можно показать, что вариограмма этой новой регуляризованной переменной:

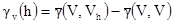[6.15]

где V_h обозначает основание V, перемещенное на расстояние h (преобразованное вектором h), а 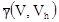представляет собой среднее значение вариограммы между произвольной точкой в V_h и другой точкой в V.

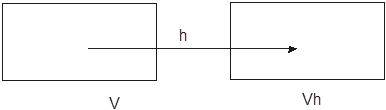
Рис 6.4. Объем V, перемещенный вектором h в объем V_h

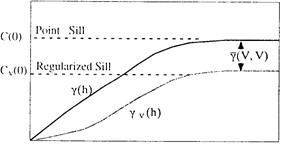
Когда расстояние h мало по сравнению с размером V, то расстояние от произвольной точки в V до произвольной точки в V_h может значительно меняться. Например, если V – прямоугольник с длиной l, то горизонтальные расстояния меняются от H-l до h+l. Однако, когда длина h значительно больше размера V, то все расстояния довольно близки к h. Следовательно, среднее значение вариограммы 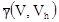приблизительно равно g(h). Поэтому мы определим зависимость:

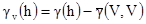{6.16]

Рис 6.5. Вариограмма с точечным основанием и регуляризованная вариограмма