Упражнение: Обычный кригинг блока

Рис 7.1. Конфигурация данных с оцениваемым блоком

Оценим кригингом выделенный блок (200м на 200м), используя 5 проб из регулярной 200м сетки. Предположим, что пространственная переменная стационарна с изотропной сферической вариограммой с порогом 2.0 и зоной 250м. Чтобы сделать возможными вычисления на карманном калькуляторе, ниже даны значения 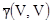и .

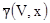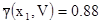
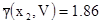
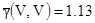[7.17]

Решение

Первый шаг – это написать систему кригинга. Так как проб 5, то система имеет размерность 6 на 6.

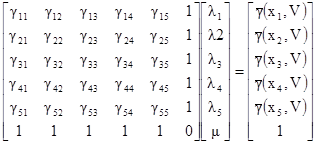[7.18]

В матричном виде находим расстояния между точками и, затем оцениваем соответствующие значения вариограмм. Например, для 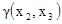расстояние между точками равно 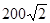. Так как эта величина больше зоны, то значение вариограммы равно порогу. В результате система принимает вид:

[7.19]

Отсюда легко получим:

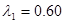
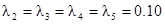[7.20]

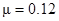
Поэтому оценка среднего значения в квадрате:

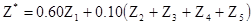[7.21]

Дисперсия оценки:

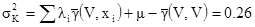[7.22]

Эффект самородка привносит элемент сложности при создании матрицы кригинга. Если, как в предыдущем случае, при сферической вариограмме эффект самородка был равен 1.5, то все недиагональные элементы матрицы увеличиваются на 1.5, а диагональные элементы остаются равными 0. Наоборот, если система записывается в элементах ковариации, то диагональные элементы будут равны суммарному порогу, включая компонент эффекта самородка; недиагональные элементы при этом остаются прежними.