Кригинг значения среднего

В обычном кригинге целью является оценивание линейной функции пространственной переменной, например - содержания в точке или среднее содержание по блоку. Здесь целью оценивания является значение неизвестного среднего m. Если мы будем использовать индекс m для того, чтобы отличать веса в этой оценке от предыдущей, то основное уравнение можно записать так

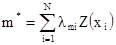[7.23]

Как и раньше эта оценка должна быть несмещенной, и дисперсия ее должна быть минимальной. Чтобы быть несмещенной, ошибка оценивания должна иметь математическое ожидание = 0. Т.е.

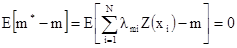
Так как среднее Z(x) есть m, то это условие можно записать, как

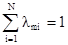[7.24]

Дисперсия ошибки оценивания –

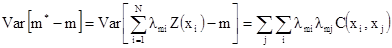[7.25]

Как и в обычном кригинге, эта дисперсия минимизируется с использованием коэффициентов Лагранжа. Следовательно, оценки кригинга –

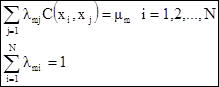[7.26]

Можно вычислить соответствующую дисперсию кригинга. Интересно, что в этом случае она равна коэффициенту Лагранжа.

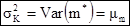[7.27]

Простой кригинг

Теперь мы построим систему кригинга, когда среднее m пространственной переменной известно. Во-первых, мы предполагаем, что пространственная переменная Y(x) имеет нулевое среднее. Понятно, что начальная пространственная переменная вычисляется из условия Z(x)=Y(x)+m. Получаем нашу оценку Y(x):

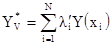[7.28]

Мы будем использовать простые числа, чтобы отличать веса простого кригинга от весов обычного кригинга и от весов для кригинга среднего. Как и раньше эта оценка должна быть несмещенной, и дисперсия должна быть минимальной. Чтобы быть несмещенной, ошибка оценивания должна иметь математическое ожидание равное 0. Т.е.

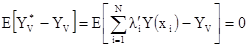[7.29]

Так как среднее Y(x) равно 0, то эта оценка автоматически становится несмещенной. Поэтому ограничение на сумму весов отсутствует. Дисперсия ошибки оценивания –

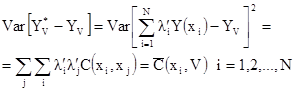[7.30]

Так как нет условия по сумме весов, то нет необходимости и в коэффициенте Лагранжа. Поэтому система кригинга имеет следующий вид

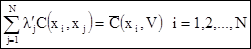[7.31]

Соответствующая дисперсия кригинга:

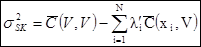[7.32]

Решение системы кригинга [7.32] дает веса кригинга и, отсюда, оценку Y_V. Оценку Z_V можно вывести заменой Y(x) на Z(x)-m. Это дает:

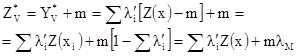[7.33]

Элемент l_M называется весом среднего в простом кригинге.

Простой кригинг редко используется в наши дни для практического применения, потому что среднее редко бывает известно. Он иногда используется на больших рудниках, например, в Южной Африке, где среднее каждой части залежи известно, потому что она разрабатывается уже много лет. Он также используется при кригинге преобразованных данных (например, после преобразования Гаусса), когда среднее устанавливается директивно, обычно – в виде нуля. Пример - дизъюнктивный кригинг. Но более важной причиной для изучения простого кригинга является то, что вес среднего – это один из лучших критериев для проверки качества кригинга. Больше информации об этом критерии качества дано в Главе 8.

Глядя на оценку [7.33], становится понятно, что форма оценщика изменилась. Сравнивая его с обычным кригингом и кригингом среднего, становится понятным, что это не больше, чем обычная линейная комбинация данных. Добавилось одно слагаемое - константа. Иногда кригинг рассматривается в терминах проекций (Journel, 1977).