Силы инерции, действующие на тело, движущееся во вращающейся системе отсчёта.

Рассмотрим самый простой случай: шарик массой т равномерно движется со скоростью v₀ вдоль радиуса вращающегося диска. Чтобы обеспечить такое движение снабдим шарик направляющим стержнем, по которому он мог бы перемещаться без трения. Нитка, прикрепленная к шарику, позволит ему в радиальном направлении двигаться с постоянной скоростью v₀ (рис. 5.6).

Рис. 5.6

Диск вращается с угловой скоростью w. Опишем движение шарика в неподвижной инерциальной системе отсчёта S(x, y). В этой системе движение шарика складывается из двух движений: равномерного прямолинейного — по радиусу диска со скоростью v₀ и кругового движения с угловой скоростью w.

В результате сложения этих двух движений, шарик будет двигаться по криволинейной траектории — разворачивающейся спирали.

В произвольный момент времени t шарик на расстоянии r от оси вращения будет иметь радиальную скорость v₀ и касательную — тангенциальную скорость, связанную с вращением диска (wr) (рис. 5.7).

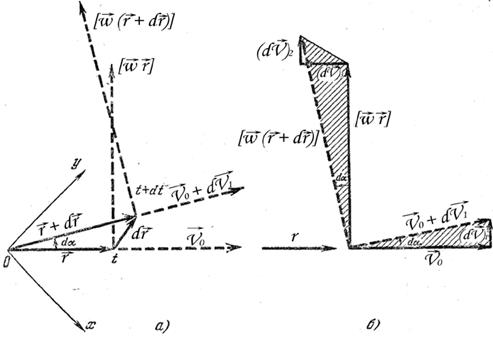
Рис. 5.7

Посмотрим, как изменятся эти скорости шарика спустя малое время dt.

Во-первых, вся картина скоростей повернётся на угол da = wdt (рис. 5.7 б). Во вторых, радиальная скорость (оставаясь неизменной по величине — V₀) получит приращение:

dV₁ = V₀da = V₀wdt, (5.5)

связанное с повтором вектора скорости V₀ на угол da = wdt.

Изменится и тангенциальная скорость. Её изменение по величине определяется тем, что шарик удалится от оси вращения на расстояние dr = V₀dt. Поэтому:

dV₂ = w(r + dr) – wr = wdr = wV₀dt. (5.6)

Кроме того, эта скорость изменится на величину:

dV₃ = wrda = wrwdt = w²rdt, (5.7)

в связи с поворотом вектора этой скорости на угол da.

Проанализировав все эти изменения, придём к выводу, что в радиальном направлении изменение скорости составит величину:

dV_r = dV₃ = w²rdt,

а в тангенциальном:

dV_t = dV₁ + dV₂ = 2wV₀dt.

Разделив эти изменения на промежуток времени dt, получим соответствующие компоненты ускорения:

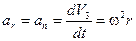; (5.8)

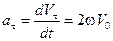. (5.9)

Несложно ответить на вопрос: какие силы обеспечивают эти ускорения?

Центростремительное ускорение создаётся упругой силой натяжения нити (F_ц.с. = F_упр. = ma_ц.с. = mw²r), направленной по радиусу к оси вращения. Касательное ускорение a_t поддерживается упругой силой деформированного стержня ( 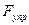= ma_t = m2wV₀). Стержень при движении прогибается и действует на шарик с силой, направленной в сторону вращения (рис. 5.8).

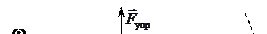
Рис. 5.8

Запишем уравнения движения шарика в инерциальной системе отсчёта. Это уравнения второго закона Ньютона для двух движений — вдоль радиуса:

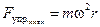, (5.10)

и в перпендикулярном направлении:

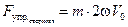. (5.11)

Теперь посмотрим, как представляется движение этого же шарика наблюдателю, вращающемуся вместе с диском.

Этот наблюдатель видит, что шарик в его вращающейся системе отсчёта движется равномерно и прямолинейно со скоростью 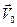= сonst вдоль радиуса диска. Ускорение шарика равно нулю, но при этом на него действует упругая сила натяжения нити F_ц.с. = mw²r и упругая сила деформированного стержня F = m2wV₀. Их равнодействующая никак не может быть равна нулю.

Для того, чтобы записать уравнение движения этого тела в неинерциальной системе отсчёта в виде уравнений второго закона Ньютона, к реально действующим упругим силам прибавим две силы инерции (рис. 5.9):

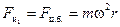(5.12)

и

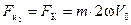. (5.13)

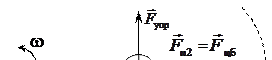
Рис. 5.9

Теперь и в радиальном и в тангенциальном направлениях суммы сил будут равны нулю, что и объясняет равномерное движение шарика вдоль радиуса.

С первой из сил инерции 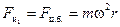мы знакомы. Это центробежная сила инерции.

Вторая сила инерции 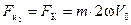называется силой Кориолиса.

Эти силы можно записать в векторном виде:

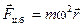
и

.

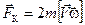Подводя итог рассмотрению движений в неинерциальных системах отсчёта, отметим следующие основные моменты.

Ньютоновским уравнением движения можно воспользоваться и в неинерциальных системах отсчёта. Но при этом систему реально действующих сил нужно дополнить силами инерции.

В неинерциальной системе отсчёта, движущейся прямолинейно и поступательно с ускорением 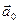, сила инерции равна:

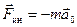. (5.14)

В неинерциальной системе отсчёта, вращающейся с угловой скоростью w, в общем случае следует ввести две силы инерции:

центробежную 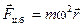, (5.15)

и кориолисову 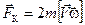. (5.16)