Сила инерции, действующая на тело, неподвижное во вращающейся системе отсчёта

Перенесём наш маятник на диск, вращающийся с угловой скоростью w вокруг вертикальной оси (рис. 5.3).

Рис. 5.3

Маятник отклонится от вертикали, двигаясь по окружности радиуса r.

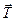Движение происходит под действием сил тяжести и натяжения нити . Их равнодействующая 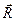, направленная по радиусу к центру окружности, обеспечивает центростремительное ускорение .

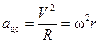Легко записать уравнение движения грузика m в неподвижной, инерциальной системе отсчёта S

R = mg ×tga = mw²r. (5.2)

Теперь перейдём на вращающийся диск и посмотрим на движение маятника в системе отсчёта, вращающейся вместе с диском S’ (рис. 5.4). Мы вновь увидим необычайную картину:

Рис. 5.4

в этой системе отсчёта маятник неподвижен. Но на него, несомненно, действует сила 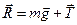, представляющая собой равнодействующую двух сил и 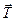. Во вращающейся, неинерциальной системе отсчёта тело, вопреки второму закону Ньютона, остаётся в покое, несмотря на действие вполне реальной силы 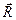. Можно воспользоваться уравнением движения Ньютона и в этом случае, если добавить к системе реально действующих сил ещё одну — силу инерции 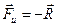(рис. 5.4). Теперь равнодействующая всех сил, действующих на тело (вместе с силой инерции) равна нулю. Поэтому тело остаётся в покое и его ускорение тоже равно нулю.

.

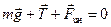Или

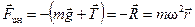. (5.3)

Во вращающейся системе отсчёта грузик маятника оказался в покое в результате действия трёх сил: силы тяжести , упругой силы натяжения нити 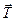и силы инерции .

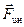Сила инерции в данном случае называется центробежной.

Центробежная сила равна центростремительной, но направлена по радиусу не к центру вращения, а в противоположную сторону — от центра.

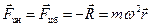
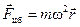(5.4)

Отметим, что центробежная сила инерции, действующая на тело, неподвижное во вращающейся системе отсчёта, зависит от положения этого тела. С увеличением расстояния до оси z, растёт и центробежная сила инерции F_цб. Это особенно хорошо видно, если разместить на вращающемся диске несколько маятников на разных расстояниях от оси вращения (рис. 5.5)

Z

Рис. 5.5