Пример применения законов Ньютона
В качестве примера рассмотрим задачу о соскальзывании небольшой шайбы с наклонной плоскости, составляющей угол a = 45° с горизонтом.

Найти коэффициент трения m шайбы о плоскость, если расстояние, пройденное телом, меняется со временем по квадратичному закону S = c × t2. Здесь с = 1.73 м/с2.
| S = c × t2 |
| с = 1.73 м/с2 |
| a = 45° |
| m = ? |
1. сделаем рисунок
2. нанесём все силы, действующие на шайбу:
сила тяжести — mg,
сила трения — Fтр = m × N,
упругая сила реакции опоры — N.
3. Выберем систему координат хy.
4. Запишем уравнение движения шайбы в векторном виде
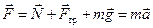
5. Спроецируем это уравнение на направления х и y, учитывая, что в направлении y ускорение отсутствует аy = 0.
х: –Fтр + mg sin a = ma (1)
y: N – mg cos a = 0 (2)
Из уравнения (2) следует, что
N = mg cos a
Используем этот результат в уравнении (1)
–m mg cos a + mg sin a = m a.
или
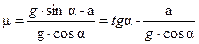 (3)
(3)
Обратимся теперь к условию S = c × t2 и найдем сначала скорость, а затем и ускорение движения.
 .
.
 . (4)
. (4)
Используя найденные результат (4) в уравнении (3), вычислим искомый коэффициент трения
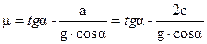
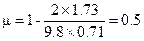

Результат, вполне ожидаемо, оказался безразмерным.
Лекция 4 «Преобразования Галилея.
Динамика системы материальных точек»
План лекции
1. Преобразования Галилея. Принцип относительности в классической механике.
2. Динамика системы материальных точек.
2.1. Закон сохранения импульса.
2.2. Теорема о движении центра масс.
2.3. Движение тела переменной массы. Реактивное движение.
Дата добавления: 2021-01-11; просмотров: 514;











