Теория о движении центра масс

Рассмотрим движение системы «n» взаимодействующих частиц.

Центром масс системы называется точка, радиус-вектор которой отвечает следующему условию

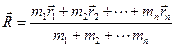(4.10)

В этом выражении 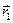, ,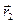…, 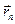— радиус-векторы элементов системы,

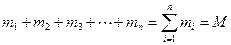— масса системы.

Продифференцировав (4.10) по времени, получим

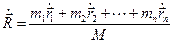
или

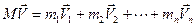
Здесь 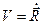— скорость движения центра масс системы. Сумма справа есть импульс нашей системы

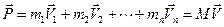(4.11)

На каждый элемент системы действуют в общем случае внутренние 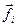и внешние 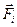силы. Поэтому уравнение 2-го закона ньютона для каждого элемента системы можно записать в таком виде

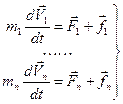
Просуммировав все уравнения этой системы, получим

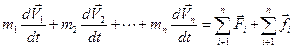
Как уже обсуждалось, векторная сумма всех внутренних сил системы равна нулю (следствие 3-го закона Ньютона)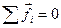

Сумма внешних сил — их равнодействующая 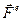— определяет скорость изменения импульса системы

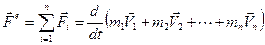
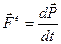(4.12)

Отметим, ещё раз, что при отсутствии внешних сил 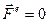, то есть в случае замкнутой системы, импульс системы не меняется

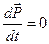и

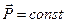
Также импульс системы будет оставаться постоянным и в случае действия внешних сил, если их равнодействующая равна нулю (это незамкнутая система). Используем результат (4.12) в уравнении движения точки центра масс системы (4.11):

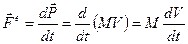
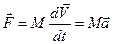(4.13)

Полученный результат формально схож с уравнением 2-го закона Ньютона для частицы. Но здесь речь идет не о частице, а о движении фиктивной точки — центра масс системы: центр масс системы движется как материальная точка, масса которой равна массе всей системы, а действующая сила — геометрической сумме всех внешних сил, действующих на систему (теорема о движении центра масс)