Закон всемирного тяготения. Сила тяжести. «Инертная» и «гравитационная» массы

Исаак Ньютон так сформулировал открытый им закон всемирного тяготения (XVII век): между двумя любыми материальными точками действуют силы взаимного притяжения, пропорциональные произведению масс этих точек и обратно пропорциональные квадрату расстояния между ними (рис. 3.4):

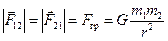. (3.7)

Здесь G = 6.65 × 10^–11 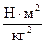— гравитационная постоянная.

Это очень малая величина, поэтому два тела, например, равных масс m₁ = m₂ = m = 1 кг на расстоянии r = 1 м притягиваются друг к другу с силой порядка 10^–10 Н!

Вот почему экспериментально в лабораторных условиях проверить закон всемирного тяготения удалось лишь в 1798 году.

Поставил этот уникальный эксперимент замечательный английский физик лорд Кавендиш.

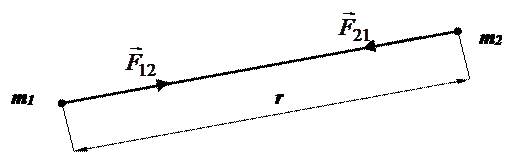
Рис. 3.4

Сила гравитационного притяжения становится заметной, когда хотя бы одно из взаимодействующих тел обладает значительной (огромной) массой — как, например, Земля. Гравитационная сила, действующая в этом случае на тело со стороны Земли, называется силой тяжести (рис. 3.5):

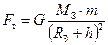. (3.8)

Здесь R_З = 6400 км — радиус Земли; h — высота тела над поверхностью.

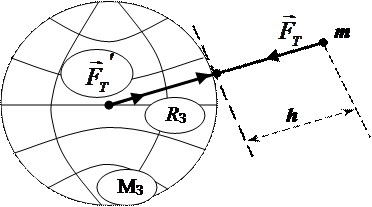
Рис. 3.5

Эта сила достигает максимального значения на поверхности Земли (h = 0) и убывает по мере увеличения высоты h. При «небольших высотах», то есть когда h « R_З, силу тяжести можно записать проще, объединив все постоянные величины в одну константу:

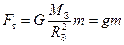, (3.10)

где 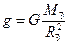= 9.8 .

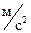Из полученного результата следует, что g — ускорение, с которым тело падает на поверхность Земли под действием только силы тяжести:

.

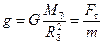Такое движение называется свободным падением, а g — ускорением свободного падения.

В законе всемирного тяготения массы взаимодействующих тел являются количественной мерой их свойства притягиваться друг к другу. Совсем не очевидно, что эти массы — «гравитационные» — совпадают с «инертными» массами, которые служат мерой иного свойства тел — их инертности.

На вопрос о соотношении этих масс ответ может дать только эксперимент. К этой экспериментальной задаче в разные годы обращались многие учёные. Среди них Ньютон, Бессель, наш соотечественник Крылов и другие исследователи. Результаты их опытов свидетельствуют о совпадении «инертной» и «гравитационной» масс. В теории относительности этот результат получил статус закона: «закон об эквивалентности инертной и гравитационной масс тела».

Силы трения

Классифицируя силы трения, прежде всего, разделяют сухое и вязкое трение (рис. 3.6).Первое возникает между сухими твёрдыми поверхностями тел, а второе — при движении в вязкой среде, либо при относительном движении тел, разделённых смазочным слоем.

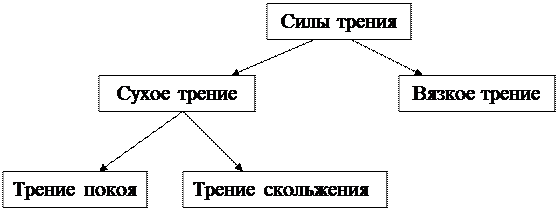
Рис. 3.6

При сухом трении, в свою очередь, различают трение покоя и трение скольжения.

Сухое трение

Приложим «небольшую» силу к телу, лежащему на горизонтальной поверхности. «Небольшую» — то есть, недостаточную для начала движения. Тело будет оставаться в покое, потому что кроме приложенной нами силы 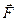на тело будет действовать равная и противоположно направленная сила трения. Это и есть «сила трения покоя» (рис. 3.7). Тело будет оставаться в покое при изменении направления приложенной силы 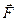и, в известных пределах, её величины. Это означает, что с изменением силы 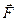будет меняться величина и направление силы трения покоя.

Увеличивая приложенное усилие 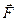, мы будем наблюдать рост силы трения покоя. Однако, этот рост не безграничен. Когда сила трения покоя достигнет своего предельного значения 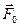, начнётся скольжение тела по поверхности. Максимальная сила трения покоя 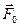зависит от материала контактирующих поверхностей, качества их обработки и от величины силы, прижимающей тело к поверхности — силы нормального давления N.

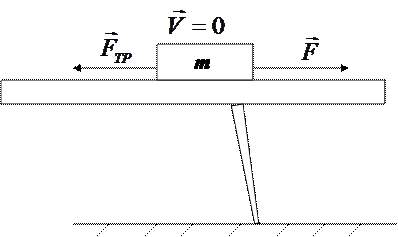
Рис. 3.7

Если приложенная сила F превышает F₀, тело будет двигаться с ускорением, пропорциональным равнодействующей силы F и силы трения — теперь уже скольжения — F_тр.

Согласно опытному закону Амонтона (1699) максимальное значение силы трения покоя F₀ и сила трения скольжения 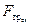пропорциональны величине силы нормального давления, прижимающей трущиеся поверхности друг к другу N:

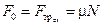. (3.11)

Здесь m — коэффициент сухого трения. Это табличная величина, связанная как уже отмечалось, с материалом трущихся поверхностей и качеством их обработки.

Сила трения скольжения не зависит от площади поверхности соприкосновения тел.

Вязкое трение

Сила вязкого трения действует на тело, движущееся в вязкой среде (жидкой или газообразной). Она зависит от формы и размеров тела, скорости его движения, а также от физических свойств среды: в частности — от плотности r и вязкости m.

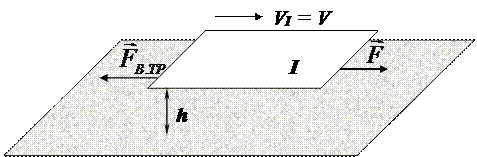Ньютон экспериментально исследовал силу вязкого трения, возникающую при относительном скольжении двух поверхностей I и II, разделённых слоем жидкости (рис. 8).

Рис. 3.8

Эта сила оказалась пропорциональной скорости V подвижной пластины I, её площади S и обратно пропорциональной толщине h разделительного слоя жидкости:

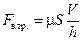. (3.12)

Здесь m — вязкость жидкости, [Па × с].

В 1851 году английский физик Джордж Стокс рассчитал силу вязкого сопротивления, действующую на твёрдый шар радиуса r при его медленном поступательном движении в неограниченной вязкой среде:

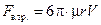. (3.13)

Эта формула известна как закон Стокса.

Покажем, как, используя этот закон, можно экспериментально определить вязкость жидкости m.

На шар радиуса r, падающий в вязкой среде будут действовать три силы (рис. 9): сила тяжести P = r_тgV, сила вязкого сопротивления F_в.тр. = 6pmrv и сила гидростатического выталкивания (Архимеда) F_Арх. = r_жgV. Здесь 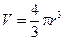— объём шара.

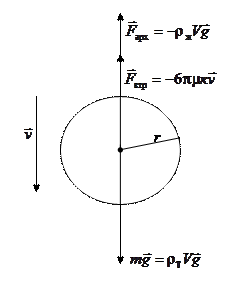
Рис. 3.9

Под действием этих сил движение шара будет происходить с ускорением:

.

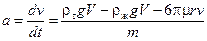Важно подметить, что в числителе этого выражения первые два слагаемых остаются постоянными, а третье в процессе движения увеличивается по мере роста скорости шара v.

При этом ускорение будет уменьшаться и станет равным нулю, когда равнодействующая сил (числитель) обратится в ноль:

r_тgV – r_жgV – 6pmrv₀ =0 (3.14)

Далее движение будет происходить с неизменной скоростью v₀.

Решим последнее уравнение относительно коэффициента вязкости m:

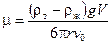(3.15)

Для вычисления вязкости жидкости m нужно измерить r_т и r_ж — плотность вещества шара и жидкости; r и v₀ — радиус шара и скорость его равномерного падения в среде. Конечно, придётся вычислить и объём шара V = 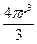. Эта простая методика измерения вязкости и сегодня широко используется в «вискозиметрах Стокса».