Упругие силы. Закон Гука

Упругими называются силы, возникающие при упругих деформациях тел.

Рассмотрим зависимость деформации металлического стержня или струны от величины внешней растягивающей силы F (рис. 3.10). Удлинение стержня будет зависеть не только от величины приложенной силы, но и от его начальной длины — l₀, поэтому в качестве объективной характеристики деформации тела принимается его относительное удлинение:

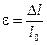. (3.16)

Относительное удлинение будет одинаковым как для разных участков стержня, так и для всего стержня в целом. Эта величина будет зависеть теперь только от приложенной силы.

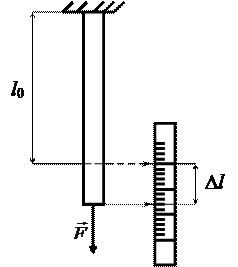
Рис. 3.10

Считается, что растягивающая сила равномерно распределена по поверхности любого поперечного сечения стержня S. Отношение 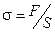называется напряжением. Напряжение измеряется в 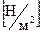и численно равно силе, действующей на поверхности единичной площади. На графике (рис. 3.11) представлена зависимость относительной деформации e от напряжения s.

Рис. 3.11

Вначале с увеличением растягивающего усилия F деформация стержня растёт пропорционально напряжению (до точки П на графике). При дальнейшем увеличении нагрузки пропорциональность нарушается, стержень удлиняется при почти неизменной нагрузке. Эта область — за точкой Т диаграммы называется областью текучести. Здесь происходят пластические, необратимые деформации, которые не исчезнут бесследно после снятия нагрузки. Дополнительное увеличение нагрузки приводит к разрыву стержня (т.Р).

Упругие силы возникают при деформациях стержня только в пределах области пропорциональности. Здесь напряжение пропорционально относительной деформации

s = Е ´ e (3.17)

Эта важная зависимость была установлена в 1660 году английским учёным и изобретателем Робертом Гуком. Коэффициент пропорциональности Е в законе Гука — модуль Юнга — является одной из характеристик материала.

Отметим, что всё сказанное справедливо, конечно, и для случая сжатия стержня.

Перепишем закон Гука в таком виде

,

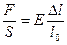F = k ´ Dl, (3.18)

где: 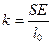— коэффициент упругости.

В этой форме закон Гука записывают и для случая упругой деформации пружин

Е = к × х, (3.19)

здесь: х — деформация пружины,

F — приложенная внешняя сила (рис. 3.12).

X

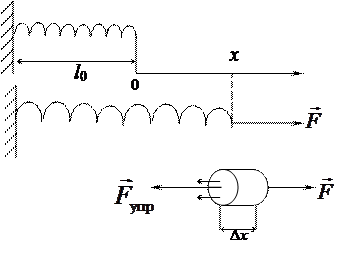
Рис. 3.12

Если рассмотреть малый элемент пружины Dх, то окажется, что он находится в равновесии потому, что кроме внешней силы на него действует равная по величине и противоположная по направлению упругая сила

F_упр = –F = –к × х

Упругая сила, возникающая при деформации тела, прямо пропорциональна величине деформации х тела. Знак минус означает, что упругая сила направлена всегда к положению равновесия.