Преобразования Галилея. Принцип относительности в классической механике

«Если среди систем отсчёта движущихся друг относительно друга прямолинейно, равномерно и поступательно, есть хотя бы одна инерциальная, то и все остальные системы тоже инерциальные».

Это положение, сформулированное Галилеем, является основным утверждением принципа относительности в классической механике.

Главная особенность инерциальных систем отсчёта состоит в том, что динамические законы механики — законы Ньютона — во всех таких системах имеют одинаковый вид. Кинематика одного и того же движения в разных инерциальных системах может быть разной, а законы динамики остаются неизменными.

Рассмотрим две системы отсчёта: S(x, y, z) и S’(x’, y’, z’): одна из них — S(x, y, z) — инерциальная, а другая — S’(x’, y’, z’) — движется относительно первой с неизменной скоростью поступательного движения 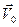. Примем для простоты, что в начальный момент времени они совпадали.

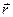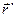Запишем движение точки М в этих двух системах, задав это движение радиус-векторами и соответственно в системе S и S’ (рис. 4.1).

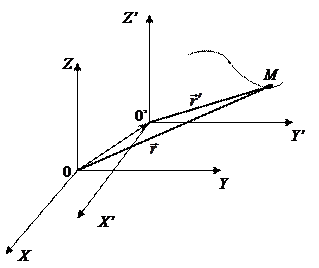
Рис. 4.1

Эти радиус-векторы связаны простым соотношением:

.

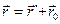Здесь 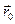— радиус-вектор, определяющий положение точки О’ системы S’ в системе отсчёта S.

Понятно, что к моменту времени t:

.

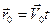Таким образом,

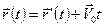. (4.1)

Это первая формула преобразованийГалилея.

Спроецировав (4.1) на координатные оси, запишем это преобразование в скалярной форме:

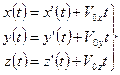(4.2)

В классической механике формулы преобразования координат (4.1) и (4.2) дополняются утверждением, что время в обеих системах отсчёта течёт одинаково:

t = t’. (4.3)

Таким образом, формулы преобразований предполагают абсолютность длин и времени в нерелятивистской классической механике.

При переходе из одной системы в другую, координаты движущейся точки меняются (4.2). Параметры, обладающие таким свойством, называются вариантными. Время в обеих системах отсчёта остаётся одинаковым, то есть время — инвариант.

Будет ли меняться при переходе в новую систему отсчёта скорость движущейся точки М?

Для ответа на этот вопрос рассмотрим первую производную радиус-вектора (4.1) и координат точки (4.2) по времени:

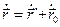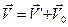, (4.3)

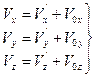(4.4)

Формулы (4.3) и (4.4) выражают нерелятивистский закон сложения скоростей. Здесь 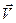— скорость частицы М в системе отсчёта S. 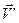— скорость в системе отсчёта S’. 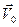— скорость штрихованной системы отсчёта относительно инерциальной системы S. Скорость оказывается разной в разных системах отсчета, т.е. она вариантна.

Дифференцируя (4.3) ещё раз по времени, получим:

,

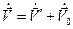здесь последнее слагаемое равно нулю, так как скорость движения системы S’ по условию постоянна. Значит:

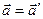. (4.5)

Этот результат означает, что ускорение инвариантно относительно преобразования Галилея. Координаты движущейся частицы, её скорость различны в разных системах отсчёта, а ускорение остаётся неизменным при переходе из системы S в систему S’.

Если система S инерциальна, то свободная частица в ней движется без ускорения, то есть, а = 0. Но ускорение такой частицы и в штрихованной системе будет отсутствовать: ведь а’ = а =0! Это означает, что она тоже является инерциальной.

Сила, действующая на частицу в системе S может быть записана так:

.

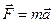А в системе штрихованной та же сила должна быть представлена иначе:

.

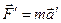Так как ,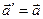

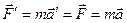. (4.6)

Это уравнение означает, что второй закон Ньютона не меняется при переходе в штрихованную систему отсчёта. То есть, уравнения классической механики Ньютона инвариантны относительно преобразования Галилея.

В этом состоит принцип относительности Галилея, утверждающий, что все три закона динамики справедливы во всех инерциальных системах отсчёта.