Ускорение. Нормальное и тангенциальное ускорение. Радиус кривизны траектории

Движение по криволинейной траектории всегда происходит с переменной скоростью. Пусть 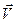— скорость частицы в момент времени t, а 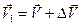— скорость частицы Dt секунд спустя.

Отношение вектора изменения скорости 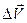к промежутку времени, за который это изменение произошло, определяет вектор среднего ускорения движения

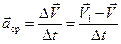(2.11)

.

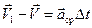Вектор среднего ускорения всегда направлен в сторону вогнутости траектории (рис. 2.11)

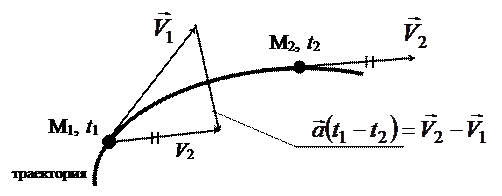
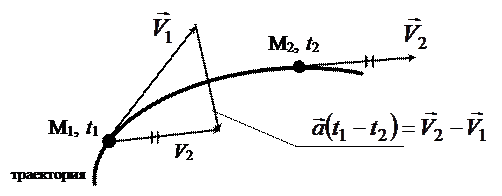
Рис. 2.11

Предел среднего ускорения при Dt ® 0 называется вектором мгновенного ускорения частицы в момент времени t.

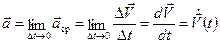. (2.12)

Скорость можно представить векторной суммой её составляющих (см. (2.10))

.

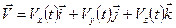Тогда вектор ускорения можно записать так:

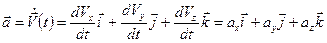. (2.13)

Здесь , , .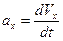

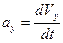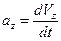Модуль вектора ускорения

.

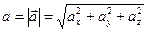Часто проецируют вектор ускорения не на оси неподвижной системы координат, а на направления касательное (t) и нормальное 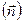к траектории (рис. 2.12):

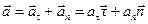. (2.14)

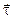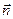Здесь а_t и а_n — проекции вектора ускорения, и — единичные векторы тангенциального (касательного) и нормального направлений.

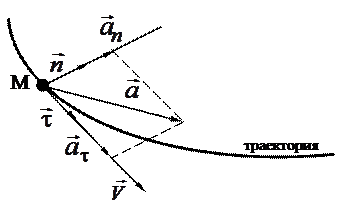
Рис. 2.12

Смысл такого представления ускорения (2.14) в том, что тангенциальное ускорение а_t определяет изменение вектора скорости только по величине, а нормальная составляющая а_n связана с изменением вектора скорости только по направлению. Покажем, что это именно так.

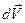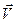Пусть за время dt скорость частицы изменилась на от до .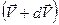

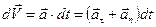(2.15)

Представим сначала, что нормальное ускорение отсутствует 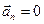. Тогда изменение скорости связано только с тангенциальным ускорением:

.

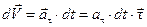Полученный результат означает, что изменение скорости 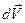совпадает по направлению с самой скоростью !

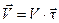Таким образом, скорость, сохраняя свое направление, будет меняться только по величине

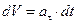
или

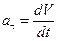(2.16)

Касательная составляющая ускорения равна производной модуля скорости по времени.

Теперь пусть отсутствует касательное ускорение 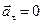. В этом случае:

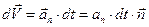
Новое значение скорости равно:

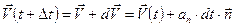
Возведем эту скорость в квадрат

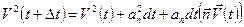
В правой части этого уравнения вторым слагаемым можно пренебречь по сравнению с V²(t), а в третьем слагаемом скалярное произведение взаимно-перпендикулярных векторов равно нулю. Таким образом, за время dt скорость частицы не изменилась по величине

!

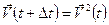Это означает, что нормальная составляющая ускорения 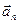определяет изменение вектора скорости только по направлению. Известно, что численно нормальное (центростремительное) ускорение равно отношению квадрата линейной скорости к радиусу кривизны траектории R:

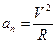. (2.17)

Чтобы пояснить этот параметр R, рассмотрим небольшой фрагмент плоской криволинейной траектории. В близких точках М и М’ проведём касательные к траектории t и t’, а к ним восстановим перпендикуляры N и N’ (рис. 2.13). Они пересекаются в точке C’.

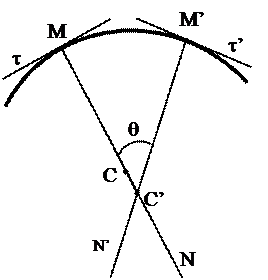
Рис. 2.13

Начнем приближать точку М’ к М. При этом угол между нормалями q и дуга 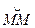устремляются в пределе к нулю. По определению радиусом кривизны плоской линии называется следующий предел

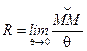(2.18)

В процессе этой операции точка C’ сместится в новое положение — точку С — центр кривизны.

Теперь обратимся к рассмотрению важного частного случая криволинейного движения.