Скалярное произведение двух векторов.

По определению скалярным произведением векторов и является число, равное произведению модулей перемножаемых векторов на конус угла между ними (рис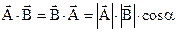. 2.5)

(2.5)

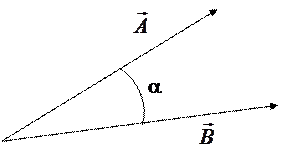
Рис. 2.5

Векторное произведение

Результатом векторного произведения векторов и является вектор 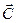, нормальный к плоскости, содержащей перемножаемые векторы.

Модуль вектора 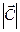равен

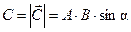. (2.6)

где: Ða —угол между векторами и 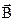(рис. 2.6).

Рис. 2.6

Направление вектора 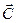= [ × 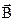] связано с направлениями перемножаемых векторов правилом правого винта.

Из определения векторного произведения следует, что модуль вектора 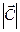равен площади параллелограмма, построенного на перемножаемых векторах. Векторное произведение некоммутативно:

[ ´ ] = – [ ´ ],

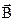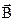то есть зависит от порядка сомножителей.

Производная вектора

Пусть вектор меняется по известному закону со временем.

.

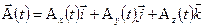Производная такого вектора по аргументу t вычисляется как производная сложной функции

где: , 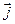и 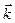— единичные векторы направлений x, y, z.

Кинематические характеристики криволинейного движения

Скорость движения

Зададим криволинейное движение частицы М зависимостью её радиус-вектора от времени (рис. 2.7):

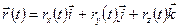. (2.7)

Рис. 2.7

Пусть 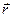и 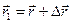— радиус-векторы частицы в моменты времени t и (t + Dt) (рис. 2.8). Разность этих векторов называется вектором перемещения частицы.

M

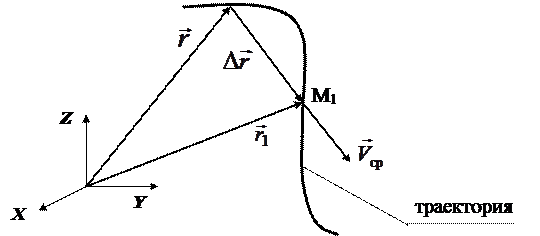
Рис. 2.8

По определению, вектором средней скорости движения в интервале времени от t до t + Dt называется отношение вектора перемещения ко времени, за которое оно произошло:

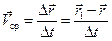. (2.8)

Направление вектора средней скорости совпадает с направлением вектора перемещения .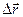

Если уменьшать интервал времени, устремляя его к нулю, то вектор средней скорости стремится к значению, которое называется мгновенная скорость:

(2.9)

Учитывая (2.7) запишем вектор мгновенной скорости в виде векторной суммы её составляющих по координатам x, y, z:

(2.10)

где: V_x, V_y, V_z — проекции вектора скорости на оси x, y, z (рис. 2.9)

Рис. 2.9

Модуль вектора скорости

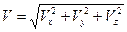
Вектор мгновенной скорости всегда направлен по касательной к траектории (рис. 2.10)

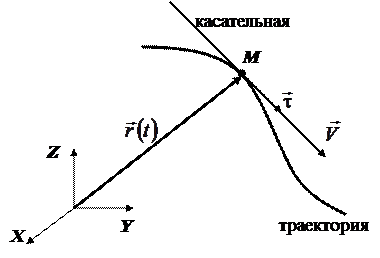
Рис. 2.10