Движение материальной точки по окружности

Положение частицы М, движущейся по окружности радиуса R, можно задать в любой момент времени углом поворота её радиус-вектора j = j(t) (рис. 2.14). Угол j отсчитывается от наперёд выбранного неизменного направления ОМ₀.

Пусть в момент времени t и (t + Dt) положение частицы на круговой траектории определяется углами j₁ и j₂. Отношение угла поворота радиус-вектора частицы Dj = j₂ — j₁ ко времени Dt, за которое произошёл этот поворот, называется средней угловой скоростью движения:

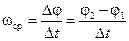. (2.19)

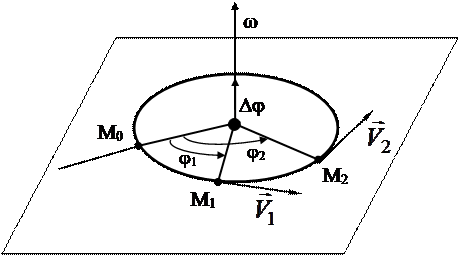
Рис. 2.14

При малом угле поворота (Dj « 2p), вводится понятие вектора угла поворота 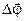. Этот вектор направлен по оси вращения и связан с направлением вращения правилом правого винта.

Угловая скорость 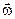— тоже вектор, совпадающий по направлению с вектором угла поворота .

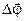Предел средней угловой скорости при Dt ® 0 — это мгновенная угловая скорость:

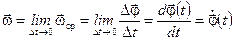. (2.20)

Мгновенная угловая скорость равна первой производной угла поворота радиус-вектора частицы по времени .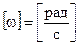

Если за промежуток времени от t до (t + Dt) угловая скорость изменилась от w до (w + Dw), то это означает, что движение происходило со средним угловым ускорением:

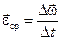(2.21)

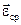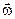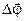Это тоже векторная величина. Вектор ускорения также как и векторы и , направлен по оси вращения.

По определению, мгновенное угловое ускорение равно первой производной вектора угловой скорости или второй производной угла поворота по времени:

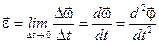(2.22)

Ясно, что круговое движение материальной точки может характеризоваться и линейной скоростью. Между линейной 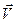и угловой 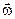скоростями должна существовать связь, поскольку речь идёт о двух подходах к описанию одного и того же движения. Найдём связь этих скоростей.

Выберем начало координат — точку отсчёта 0 — на оси вращения (рис. 2.15).

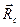— радиус-вектор движущейся точки, С — центр ее круговой траектории.

Пусть за время dt частица переместилась из точки М₁ в точку М₂; 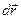— радиус-вектор её перемещения.

Линейная скорость частицы по определению .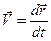

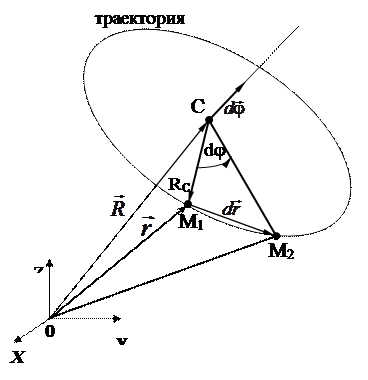
Рис. 2.15

Воспользовавшись правилом векторного произведения, представим вектор перемещения в следующем виде:

.

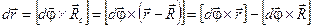Последнее слагаемое равно нулю, так как это векторное произведение двух векторов, совпадающих по направлению.

Значит, 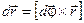, а линейную скорость тогда можно представить так:

,

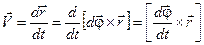или 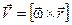, так как .

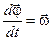В частном случае, когда начало координат — точка отсчёта 0 — находится в центре окружности — С, 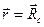и

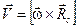. (2.23)

Поскольку 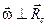, последнее выражение можно представить в скалярном виде:

V = wR_c. (2.24)

Возьмём производную этой функции по времени, учтя при этом, что R_c = const.

.

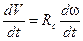Известно, что 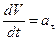, а 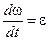. Отсюда следует простая связь тангенциальной составляющей линейного ускорения и углового ускорения при вращении по окружности радиуса R:

a_t = Re. (2.25)