Кинематика прямолинейного движения
Скорость движения
Систему координат выберем так, чтобы одна из осей (например, х) совпала с прямолинейной траекторией движения. При таком выборе две другие координаты частицы М меняться не будут y = z = 0 = сonst. (рис. 1.3).

Рис. 1.3
В этом случае движение можно задать одной скалярной функцией:
x = x(t). (1.3)
Пусть М1 и М2 — точки на траектории, которые проходит движущаяся частица в моменты времени t1 и t2, а х1 и х2 — координаты этих точек (рис. 1.4).

Рис. 1.4
Dх = х2 — х1 — расстояние, пройденное частицей за время Dt = t2 — t1.
Отношение пройденного пути Dх к затраченному времени Dt называется средней скоростью частицы:
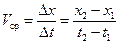 . (1.4)
. (1.4)
Если, не меняя положения точки М1, уменьшать промежуток времени Dt, то отношение 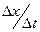 будет стремиться к определённому пределу, который называется мгновенной скоростью движения:
будет стремиться к определённому пределу, который называется мгновенной скоростью движения:
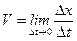 .
.
В математике такой предел называется производной функции x(t) по аргументу (t).
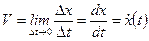 .
.
Мгновенная скорость прямолинейного движения частицы есть производная её координаты x(t) по времени:
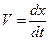 . (1.5)
. (1.5)
В системе СИ скорость измеряют в 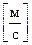 .
.
Ускорение
В общем случае прямолинейного движения скорость материальной точки может меняться во времени: V = V(t).
Пусть в момент времени t1 скорость была V1, а в момент t2 – V2 (рис. 1.5).

Рис. 1.5
Отношение изменения скорости материальной точки DV = V2 — V1 ко времени Dt = t2 — t1, за которое оно произошло, называется средним ускорением частицы в интервале времени от t1 до t2 = t1 + Dt.
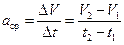 . (1.6)
. (1.6)
В пределе при Dt ® 0 среднее ускорение стремится к значению, которое называется мгновенным ускорением:
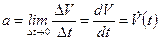 . (1.7)
. (1.7)
Мгновенное ускорение частицы равно первой производной её скорости V(t) по времени.
Так как скорость является первой производной координаты по времени 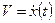 , то ускорение можно назвать второй производной координаты по времени:
, то ускорение можно назвать второй производной координаты по времени:
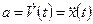 . (1.8)
. (1.8)
Ускорение в системе СИ измеряют в 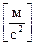 .
.
Дата добавления: 2021-01-11; просмотров: 493;











