Поиск отказавших элементов на основе чисел Фибаначи и золотой пропорции.

В математике под числами Фибаначи понимается ряд чисел [25]

1,1,2,3,5,8,13,21,…, (13.34)

В котором каждый последующий член ряда, начиная с третьего, равен сумме двух предыдущих членов.

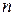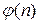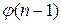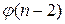Если обозначить -й член ряда через , то его связь с предидущими членами и выразиться формулой

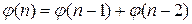(13.35)

В более общем случае является ряд 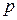-чисел Фибаначи, в котором каждый последующий член также равен сумме двух членов: предидущего и отстоящего от предидущего на 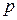шагов. Теперь, если 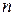-й член этого ряда обозначить через 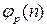, то искомая формула для членов этого ряда составит

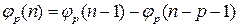(13.36)

При 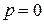из этой формулы получается «двоичный» ряд: 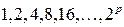при 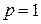- ряд Фибаначи (13.35), при 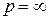имеет место следующая последовательность

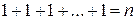
Геометрическая имтерпритация реккурентного соотношения для параметра 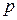для чисел Фибоначи получается в результате деления отрезка 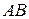точкой 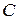на две част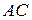и и 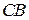, так, что

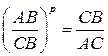(13.37)

Откуда вытекает следующее уравнение для нахождения соотношения отрезков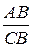

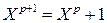(13.38)

При 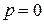(13.38) имеет единственное решение 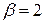, а деление отрезка отрезка 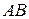точкой 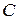является классической дихотомией ( 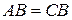), как это было рассмотрено ранее, например, на рис. 13.9. При 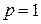положительный корень уравнения (13.38) равен

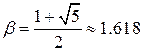(13.39)

называется золотой пропорцией, а деление отрезка 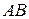точкой 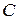в таком соотношении, называется золотым сечением или золотым 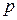- сечением.

В соответсвии с золотой пропорцией может производиться разбиение цепочки последовательно соединенных элементов при поиске неисправности. Кроме того, цепочки проверяемых элементов могут разбиваться для проведения проверок на две части, являющиеся двумя соседними числами ряда Фибаначи.

В последнем случае если число элементов не равно ближайшему члену ряда Фибаначи, то в данную цепочку добавляются фиктивные элементы, доводящие число членов ряда этой цепочки до ближайшего члена ряда Фибаначи. Пусть, после добавления фиктивных точек образовано число 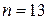, являющееся пятым членом ряда Фибаначи. Согласно данному методу первый этап контроля должен производиться в точке, разбивающей ОД на две неравные части, каждая из которых включает три и пять элементов соответственно. Если результат проверки цепочки из пяти элементов положителен, то неисправный элемент, естественно в этой группе из пяти элементов, А группа из трех элементов не содержит нисправный элемент и из дальнейших проверок исключается. Оставшийся участок из пяти элементов, согласно ряду Фибаначи разбивается на две части, состоящие из двух и трех элементов. Если при проверки в группе из двух элементов отыскивается неисправное, то проверка заканчивается обнаружением неисправного элемента. Если при проверке цепочки из трех элементов результат проверки положительный, то по аналогии с предидущим необходимо провести еще две проверки.

Если же после первоначального разбиения на три и пять элементов положительный результат дает группа из трех элементов, то цепочка из пяти элементов в дальнейшем из проверки исключается. Тем самым существенно сокращается число проверок.

При большом числе элементов разбиение из на две группы по правилу золотого сечения или по принципу двух соседних членов ряда Фибаначи практически совпадают.