Поиск неисправных элементов методом групповых проверок

Сущность метода состоит в организации последовательности таких проверок, каждый из которых позволит проверить неисправность сразу группы СЕ.

Пусть имеется система, состоящая из 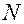произвольным образом соединенных между собой элементов с известными интенсивностями отказов 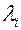. В результате контроля работоспособности системы установлено, что она неисправна. Имеется перечень возможных проверок системы 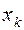, каждая из которых охватывает некоторое подмножество элементов и характеризуется своей продолжительностью 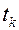. Каждая проверка имеет два исхода: положительный и отрицательный. Необходимо найти такой алгоритм поиска неисправности, при котором среднее время поиска будет минимальным.

При этом предполагается, что неисправным в ОД может быть только один элемент, а оптимальная программа поиска разрабатывается заранее, то есть еще до обнаружения неисправности.

В информационном подходе показано, что максимальное среднее количество информации о состоянии проверяемой группы элементов может быть получена, когда

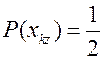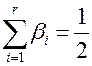; (13.27)

где 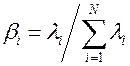-условная вероятность отказа или коэффициент отказа 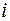-й СЕ, а 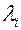- интенсивность отказа 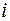-й СЕ.

Формула (13.27) означает, что речь идет о половинной разбиении, в смысле равной надежности, проверяемых групп элементов.

На практике невозможно обеспечить строго выполнение условия (13.27), поэтому обычно рекомендуется в качестве оптимальных выбирать проверки, при которых обеспечивается минимальное значения модуля разности:

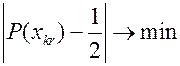(13.28)

В качестве примера составления оптимального алгоритма поиска неисправности методом групповых проверок рассматривается объект состоящий из пяти элементов, функциональные связи между которыми изображены на рис. 13.13.

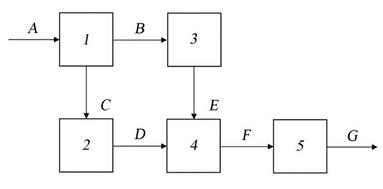
Рис. 13.15. Структурная схема объекта

Буквами A, B, C, D, E, F, G обозначены входные и выходные сигналы СЕ ОД. Известны коэффициенты отказов СЕ: ; ; ; ; .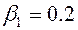

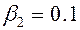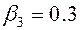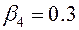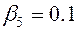Требуется определить алгоритм поиска неисправного СЕ, обеспечивающий минимальное среднее количество проверок.

Перечень возможных проверок ОД представлен в таблице 13.3. Каждой проверки присвоен двоичный код, в котором единицы указывают на проверяемые СЕ, а нули на СЕ не охваченные проверкой. В последней графе таблицы приведены значения – вероятности отрицательных проверок 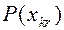, т.е. проверок, в ходе которых в проверяемой группе обнаружен неисправный СЕ. Вероятности 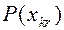рассчитываются по формуле:

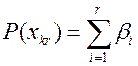, (13.29)

где 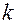- номер проверки, 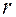- число СЕ, охватываемых этой проверкой, 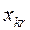- отрицательный исход проверки.

Таблица 13.3.

	Входной сигнал	Выходной сигнал	Код проверки (элементы)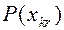
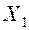
	A	B						0,2
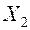
	C	D						0,1
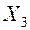
	B	E						0,3
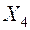
	ED	F						0,3
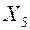
	F	G						0,1
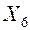
	A	D						0,3
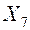
	A	E						0,5
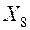
	BD	F						0,6
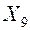
	A	F						0,9
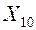
	CE	F						0,4
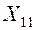
	CE	G						0,5
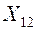
	E	G						0,4

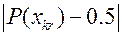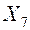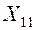На первом этапе разработки алгоритма анализируется информация, содержащиеся в последнем столбце таблицы 13.3. Анализ показывает, что минимальное значение модуля обеспечивают проверки и . Пусть в рассматриваемом случае легче организовать проверку 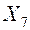, тогда она и будет первой проверкой искомого алгоритма. При положительном исходе этой проверки (неисправного СЕ) среди проверенных 1-го и 3-го СЕ нет) необходимо перейти к поиску неисправного СЕ в группе 2,4,5 (проверка 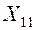), а при отрицательном исходе проверки 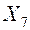среди СЕ 1 и 3.

Так как алгоритм поиска составляется заранее и неизвестно, чем закончиться проверка 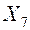, то на втором этапе его разработки определяются последующие проверки для всех возможных исходов, т.е. для каждой из названных групп элементов. Эти в дальнейшем рассматриваются как самостоятельные объекты, для каждой из которых естественно должно обеспечиваться выполнение услови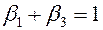й

и 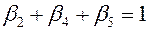. (13.30)

Так как из последней графы таблицы 13.3 уже известно, что

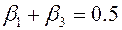и 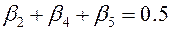. (13.31)

(проверк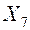и и 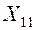соответственно), то условие (13.30) может быть выполнено если обе части выражений (13.31) разделить на 0.5., т.е. выполнить условие нормировк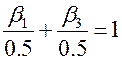и

и 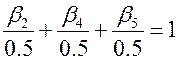. (13.32)

Введя новые обозначения для коэффициентов отказов (13.32), можно записать

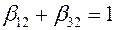и 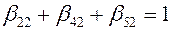. (13.33)

Где первые индексы обозначают номер СЕ, а вторые – номер очередного этапа разработки алгоритма. С учетом выражения (13.32) и (13.33) можно определить

; ; ; ;

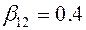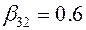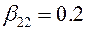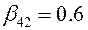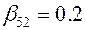
Перечень возможных проверок для группы 1 и 3 и группы СЕ 2,4,5 на втором этапе составления алгоритма, приведены соответственно в таблицах 13.4 и 13.5.

Если на первом этапе отрицательный исход получен при проверке элементов 1 и 3 (см. табл. 13.5), то на втором этапе безразлично с какого элемента его начинать. Так как любой исход при проверке одного из этих СЕ однозначно определяет неисправность.

Таблица 13.4

Проверка	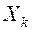Код проверки (элементы)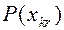
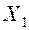
			0.4
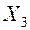
			0.6

Таблица 13.5

Проверка	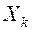Код проверки (элементы)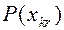
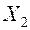
				0.2
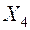
				0.6
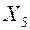
				0.2
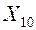
				0.8
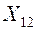
				0.8

Из анализа таблицы 13.5? что наиболее информативной является проверка 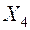, следовательно, ее и надо включать в алгоритм поиска неисправного СЕ. При отрицательном исходе проверки 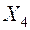однозначно будет определена неисправность четвертого элемента, а при положительном исходе этой проверке необходимо перейти к проверкам группы СЕ 2 и 5. Поскольку в этой группе только два элемента порядок их проверки безразличен. Можно выбрать например проверку 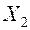, в результате которой будет выявлена неисправность СЕ 2 или 5. Таким образом, формируется алгоритм проверок, позволяющий обнаружить неисправность любого СЕ при минимальном числе проверок.

Графически этот алгоритм можно представить в виде диаграммы (рис. 13.11).

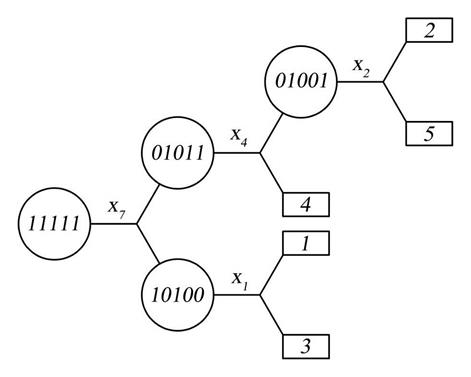
Рис. 13.16. Диаграмма алгоритма проверок

Горизонтальными линиями на диаграмме (рис. 13.11) изображены проверки. Над линиями на диаграмме располагаются условные обозначения проверок, а под ними – продолжительности проверок, если они известны. От каждой проверки идут два расходящихся луча, заканчиваются кружком или прямоугольником, содержание которых отражает знания о состоянии системы, получаемые при возможных исходах проверки. Исходные знания о системе также изображаются кружком. Знания о состоянии системы представлены в виде двоичных кодов. Единицами в применяемом коде обозначены элементы, которые могут быть неисправными, а нулями – исправные элементы. Так кодом 11111 обозначено исходное состояние системы, т.е. то, что система неисправна и неисправным может оказаться любой (но только один) ее элемент. Кружок с кодом 01011 обозначает данные о состоянии системы после того, как в результате проверки 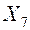выяснилось, что в первый и третий, элементы исправны. Диаграмма проверок обрывается, если в результате очередной проверки будет получена полная информация о состоянии системы, т.е. будет найден неисправный элемент. Такой исход проверки обозначен прямоугольником, в котором указан номер неисправного элемента.