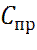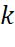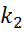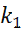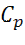Оптимизация программы испытаний сложных объектов по стоимости
Современные сложные технические объекты состоят, как правило, из нескольких автономных элементов. Поэтому испытанию объекта в целом предшествует испытания составляющих его элементов (см. рис.12.1. и 12.2).
Одним из возможных путей сокращения расходов на испытания и отработку объекта является применение так называемой ступенчатой программы испытаний, то есть испытаний с последовательным наращиванием числа испытываемых элементов в соответствии с их функциональным назначением. Подобный подход позволяет сократить как стоимость испытаний объекта, так и время, затрачиваемое на отработку объекта.
Например, испытания многоступенчатых ракет-носителей или ракет космического назначения (РКН) может проводится с последовательным наращиванием «верхних» ступеней по мере отработки «нижних» ступеней. Действительно, одной из основных задач испытаний РКН является обеспечение безотказности 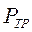 РКН в целом, однако в данной ситуации полезная информация о работоспособности и надежности не начавших функционировать «верхних» ступеней РКН отсутствует.
РКН в целом, однако в данной ситуации полезная информация о работоспособности и надежности не начавших функционировать «верхних» ступеней РКН отсутствует.
Таким образом, программа неполных испытаний РКН состоит в том, что до тех пор, пока нет обоснованной уверенности в достаточно надежном функционировании первой ступени, нет смысла проводить испытания полноразмерной РКН, поскольку при отказе первой ступени будут выходить из строя все последующие «верхние» ступени. Поэтому целесообразно проводить неполные испытания РКН, в которых на первом этапе испытывается первая ступень, а все последующие «верхние» заменяются макетами, обладающими соответствующими аэродинамическими и весогабаритными характеристиками.
Практика построения ступенчатой отработки ЛА нашла достаточно широкое распространение. Так, например, в США при отработке ракет «Минитмен», «Атлас», «Титан» и др. число неполных пусков составляло в среднем 8…11[25].
Программа построения программы ступенчатой отработки может быть построена на основе полученных ранее уравнений отработки (12.46), (12.47), называемых кривыми роста надежности [1-5]. Параметрами этих уравнений являются значения начальных показателей безотказности 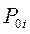 ступеней РКН, поступающих на испытания, и показатели
ступеней РКН, поступающих на испытания, и показатели 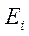 эффективности отработки характеризующих вероятность выявления и устранения i-ой причины отказа или дефекта. В дальнейшем под надежностью ступени и РКН в целом понимается вероятность их безотказного функционирования в полете.
эффективности отработки характеризующих вероятность выявления и устранения i-ой причины отказа или дефекта. В дальнейшем под надежностью ступени и РКН в целом понимается вероятность их безотказного функционирования в полете.
С учетом сказанного возможность количественного описания программы ступенчатых испытаний РКН может быть реализована следующим образом. Так, надежность 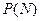 РКН, состоящем из S ступеней после проведения N летных испытаний запишется в виде
РКН, состоящем из S ступеней после проведения N летных испытаний запишется в виде
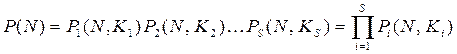 , (12.54)
, (12.54)
где 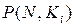 - уравнение отработки i-ой ступени РКН;
- уравнение отработки i-ой ступени РКН;
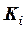 - число испытаний с макетами i-ой,
- число испытаний с макетами i-ой, 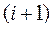 -ой, …, S-ой ступеней.
-ой, …, S-ой ступеней.
Выражение (12.54) предполагает, что неполные испытания проводятся последовательно: на первом этапе проводятся подряд только 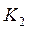 испытаний первой ступени (поскольку в данном случае использование макетов первой ступени не предусматривается, то
испытаний первой ступени (поскольку в данном случае использование макетов первой ступени не предусматривается, то 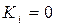 ), на втором этапе подряд проводятся
), на втором этапе подряд проводятся 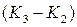 испытаний РКН, состоящего из 1-ой и 2-ой ступеней с макетом 3-ой ступени и т.д.
испытаний РКН, состоящего из 1-ой и 2-ой ступеней с макетом 3-ой ступени и т.д.
Общая стоимость C такой программы испытаний, определяемой выражением (12.54), составит
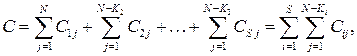 (12.55)
(12.55)
где 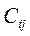 - стоимость испытания i-ой ступени на проведение испытания с номером j, включающего стоимость самой i-ой ступени с учетом стоимости макета(ов) и дополнительных затрат на организацию неполных испытаний.
- стоимость испытания i-ой ступени на проведение испытания с номером j, включающего стоимость самой i-ой ступени с учетом стоимости макета(ов) и дополнительных затрат на организацию неполных испытаний.
С учетом (12.54), (12.55) задача оптимизации программы ступенчатой отработки (неполных испытаний), обеспечивающей заданное значение показателя безотказности 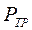 и минимизирующей стоимость программы испытаний, формируется следующим образом [10-15]
и минимизирующей стоимость программы испытаний, формируется следующим образом [10-15]
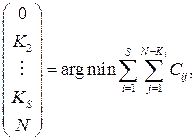 (12.56)
(12.56)
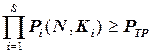 ,
,
где N, 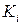 - целочисленные,
- целочисленные, 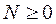 ,
, 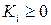 .
.
В качестве частного случая можно рассмотреть программу испытаний двухступенчатого летательного аппарата (ЛА) с K неполными испытаниями. Кроме того, предполагается, что стоимости 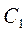 и
и 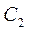 постоянные в течение всех испытаний.
постоянные в течение всех испытаний.
Тогда уравнение (12.55) преобразуется к виду
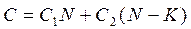 . (10.57)
. (10.57)
где 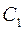 ,
, 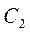 - стоимости испытаний первой и второй ступеней соответственно.
- стоимости испытаний первой и второй ступеней соответственно.
При допущении о непрерывности функций 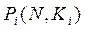 решение поставленной задачи может быть осуществлено, например, по методу неопределенных множителей Лагранжа [17-20].
решение поставленной задачи может быть осуществлено, например, по методу неопределенных множителей Лагранжа [17-20].
В этом случае функция Лагранжа принимает вид
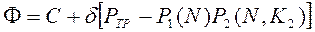 . (12.58)
. (12.58)
На основе (12.58) составляется система уравнений
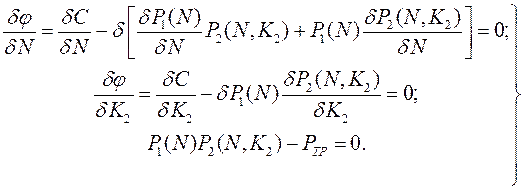 (12.59)
(12.59)
Решение системы уравнений (12.59) дает оптимальные значения параметров N и K в виде:
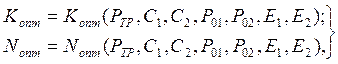 (12.60)
(12.60)
где 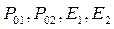 - параметры уравнений отработки ступеней ЛА, определяемые формулами
- параметры уравнений отработки ступеней ЛА, определяемые формулами
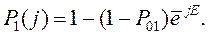
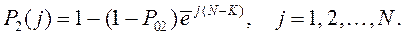
Последующая проверка полученного решения (12.60) на минимум с помощью выражений (12.57), (12.58) дает решение поставленной задачи.
Из выражения (12.57) следует, что зависимость относительной стоимости 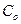 программы отработки от числа неполных пусков, определяемого из уравнения (12.58), имеет вид
программы отработки от числа неполных пусков, определяемого из уравнения (12.58), имеет вид
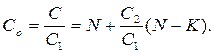 (12.61)
(12.61)
Откуда следует, что при 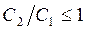 стоимость испытаний (12.21) достигает минимума при
стоимость испытаний (12.21) достигает минимума при 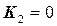 , то есть при параллельной отработке обеих ступеней в составе ЛА.
, то есть при параллельной отработке обеих ступеней в составе ЛА.
С увеличением стоимости второй ступени становится все более экономически выгодной ступенчатая отработка ЛА ( 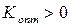 ), причем по мере увеличения отношения
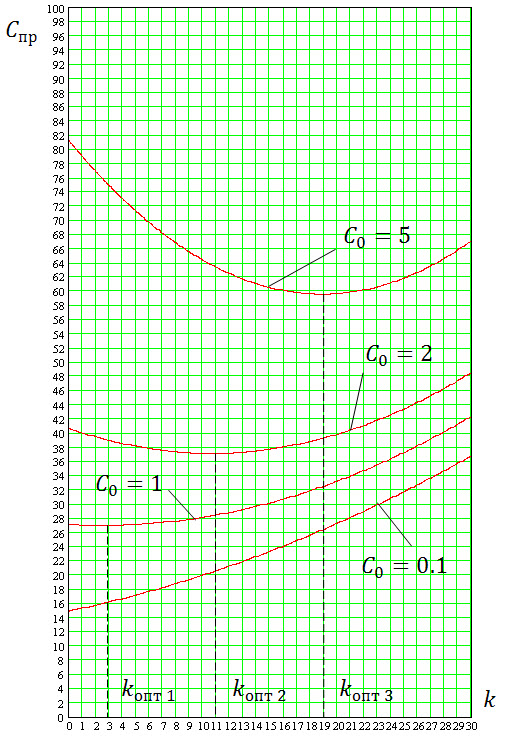
), причем по мере увеличения отношения 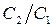 минимум стоимости сдвигается в сторону больших K, как это показано на рис. 12.15.
минимум стоимости сдвигается в сторону больших K, как это показано на рис. 12.15.
|
|
| |
| |
Рис. 12.18 Зависимость относительной стоимости программы испытаний от числа неполных пусков для значений относительной стоимости II ступени: 
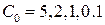 при
при 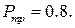
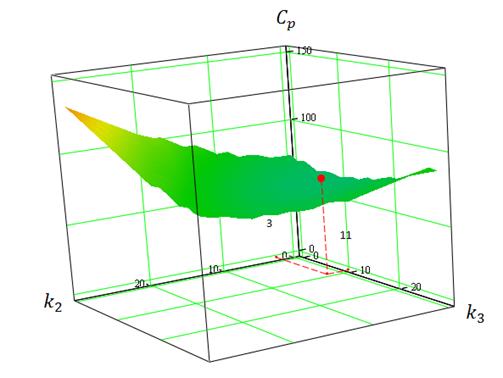
Рис. 12.19 Зависимость относительной стоимости программы испытаний от числа неполных испытаний II и III ступени для значений относительной стоимости II ступени: 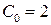 при
при 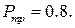




|
|
|
| |
| |

| |
Дата добавления: 2016-09-26; просмотров: 2325;