Определение числа доработок для обеспечения требуемого значения показателя надежности.

Анализ процесса изменения надежности объекта при отработке (12.37) показывает, что с увеличением числа доработок реализации процесса (12.38), (12.37) стягивается к его математическому ожиданию, а само математическое ожидание асимптотически стремится к единице. Действительно, в соответствии с определением доработки (см. п.12.1) после ее проведения объект обновляется и становится как бы новым. То же самое происходит после второй доработки и т.д. Поэтому испытание одного объекта после проведения n доработок эквивалентно испытаниям n таких же объектов без доработок. В этом случае оценка P^* математического ожидания отрабатываемого объекта и дисперсия 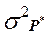этой оценки после проведения n испытаний могут быть оценены по известным формулам [1-5]

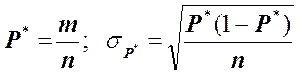, (12.48)

где m - число успешных испытаний (m<n).

Таким образом, с ростом числа испытаний оценки (12.48) стремятся (при большом числе испытаний j>30) к своим истинным значениям, поэтому процесс отработки представляется моделью математического ожидания (см. рис.12.1) при 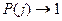, то есть описывается формулой

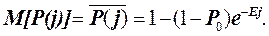(12.49)

Другими словами, реализации процесса (12.48), (12.49) стягиваются к его математическому ожиданию M[P(j)].

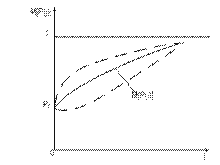
Рис.12.16. – Характер рассеивания реализаций процесса изменения показателя надежности испытываемого объекта при отработке.

Если известно требуемое значение показателя надежности, которое должно быть достигнуто по результатам испытаний, то при известных параметрах P₀ и E из формулы (12.49) можно найти требуемое число 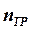испытаний

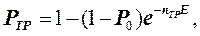
откуда после преобразований:

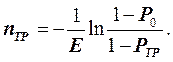(12.50)

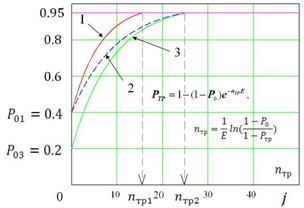
Рис. 12.17 - Анализ математического ожидания процесса роста надежности при отработке: 1 ( ),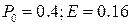

2 ( 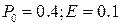), 3 ( ).

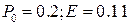На рисунке 12.14 приведены графики изменения показателей надежности объекта при различных значениях параметров P₀ и E. Из рисунка следует, что влияние параметра E на показатель надежности значительно превосходит влияние параметра P₀. Так, при существенно меньшем значении параметра P₀ (0,2 против 0,4) кривые 2 и 3 одновременно при 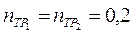достигают требуемого уровня надежности P_ТР=0,95, что получается за счет более высокой эффективности отработки E (0,11 против 0,1). С другой стороны у кривых 1 и 2 одинаковые значения параметра P₀=0,4, однако за счет более высокого параметра E=0,16 у кривой 1 требуемое значение показателя надежности P_ТР=0,95 достигается при значении 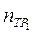существенно меньшем, чем 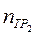(см. рис. 12.14).

Выражение для определения E может быть получено из формулы (12.42) следующим образом

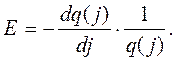(12.51)

Если перейти к конечным разностям при 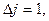то формула (12.51) преобразуется к виду

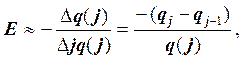(12.52)

откуда с учетом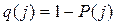

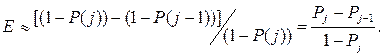(12.53)

Таким образом, параметр E представляет собой средний прирост показателя надежности по результатам одного испытания, отнесенный к оставшемуся значению показателя надежности.