Условия работоспособности объектов. Контроль работоспособности.

Состояние ОД характеризуется совокупностью диагностических признаков. Так, условия работоспособности по одному параметру непрерывных объектов задаются неравенствами, которые ограничивают его значения, например, с одной стороны:

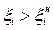(R_и > 50 Мом, сопротивление изоляции);

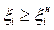(R_и 50 Мом, сопротивление изоляции);

(R_и < 50 Мом, сопротивление изоляции).

Если состояние ОД определяется несколькими диагностическими признаками, то задача контроля работоспособности сводят к проверке рассмотренных выше неравенств для каждого из параметров. Например, контроль состояния ОД может осуществляться по показателям переходной характеристики 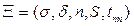(рис. 13.4):

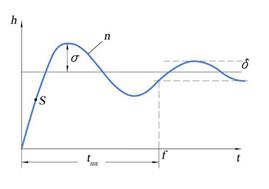
Рис. 13.5. Переходная характеристика

На рис.13.4 приянты следующие обозначения: - величина перерегулирования; - статическая точность; 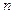- число колебаний; 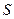- крутизна; 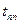- время переходного процесса

Для решения задачи контроля в этом случае необходимо задать условия работоспособности вида 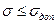, , , , 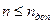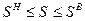(индекс “доп” означает допустимое значение).

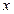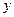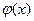Если в качестве диагностических признаков рассматривает характеристика вида , где и входныая и выходная переменные, то условия работоспособности определяются значением отклонения текущей характеристики от номинальной . При этом сходства и различия этих характеристик определяется следующими критериями:
1. Критерий среднего отклонения

.

Недостатком этого критерия является одинаковая чувствительность как к величине абсолютного отклонения, так и к длительности интервала, не котором оценивается отклонение.

2. Критерий среднеквадратичного отклонения

.

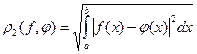Этот критерий более чувствителен к величине отклонения, чем к длительности интервала, на котором отклонение оценивается. Он наиболее часто используется на практике.

3. Критерий равномерного приближения

.

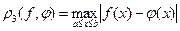При этом критерием близости является максимальное отклонения на интервале

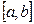. Если максимальное отклонение мало, то на всем интервале определения функции и 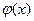будут мало отличаться друг от друга. Все эти критерии определяющие условия работоспособности ОД сводятся к неравенству 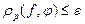где 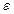от – допустимое отклонение, а – вид критерия.

В случае дискретных ОД они рассматриваются как преобразователи наборов входных воздействий в выходные , где 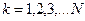. Причем 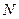при рабочем диагностировании равно числу входных рабочих воздействий. При тестовом диагностировании входные воздействия определяются из условия срабатывания всех элементов в ОД.

Каждый набор имеет вид

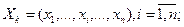
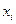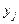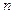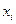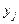где и - значения напряжений на соответствующем входе и выходе, - число входов, - число выходов. Обычно в качестве и рассматриваются сигналы 0 и 1 (0 – напряжение отсутствует, 1 – напряжение имеется). Поскольку каждому входному набору соответствует определенный выходной набор , то условием работоспособности такого дискретного ОД является соответствие всех возможных входных наборов выходным наборам ., т.е. .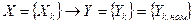

При рабочем диагностировании - рабочие воздействия.

При тестовом диагностировании для проверки условий работоспособности необходимо построить минимальную входную последовательность наборов, позволяющую оценивать состояния всех элементов объекта. Например, в случае комбинационной схемы (рис. 13.5) объект имеет четыре входа 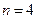, входной набор , один выход 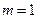, выходной набор 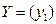реализует функцию

.

Рис. 13.6. Комбинационная схема

Проверка элементов схемы (рис.13.5) осуществляется подачей сигналов 1 на входы элемента. Для срабатывания всех элементов объекта необходимо наличие двух единиц. Этому соответствует следующая таблица состояний:

Таких наборов оказывается шесть. Из таблицы видно, что для срабатывания всех элементов объекта достаточно четырех входных наборов ( 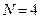), а именно 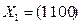, , 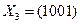, , 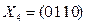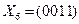или 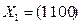, , , , 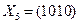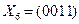так как 2-й и 3-й, 4-й и 5-й наборы адекватны по воздействию на объект. Таким образом, минимальная тестовая последовательность, достаточная для проверки условия работоспособности, включает четыре вектора 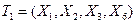или 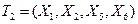, а условия работоспособности представляют соответствия

; ; ; .

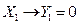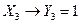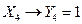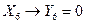Следует иметь в виду, что в объектах, охваченных отрицательно обратной связью, влияния возникшего дефекта проявляется незначительно при определении состояния ОД по выходу.

Например. Передаточная функции ОД, представленного на рис 13.7. имеет вид

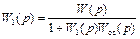, (13.1)

где 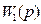- передаточная функция объекта; - передаточная функция звена с обратной связью.

Рис. 13.7. Объект диагностирования с обратной связью

После деления числителя и знаменателя правой части выражения (13.1) на 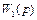имеет место

. (13.2)

Если коэффициент усиления 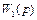по модулю велик, что характерно для реальных объектов, то можно считать, что

(13.3)

Так, если 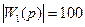, а 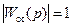, то изменение 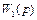на 50% изменит 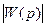с 0.9901 до 0.9804.

Таким образом, дефекты, возникающие в самом объекте по выходному сигналу, могут быть не обнаружены.

Иная картина – при наличии дефекта в цепи обратной связи.

Выходной сигнал 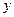связан для рассматриваемого ОД с входным следующим образом:

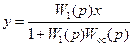. (13.4)

Если считать, что изменяется только 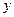и , то дифференцирование выражения (13.4) дает:

. (13.5)

Деление (13.5) на (13.4) приводит к следующему результату:

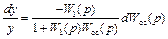. (13.6)

Так как 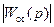значителен, то выражение (13.6) может быть представлено в виде:

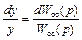(13.7)

т.е. относительное изменение выходного сигнала пропорционально относительному изменению в цепи обратной связи.

Следовательно, дефекты, возникающие в объекте, не обнаруживаются при контроле состояния по выходу. Дефекты, возникающие в цепи обратной связи, можно обнаружить при контроле выходного сигнала. В этом случае выявить наличие дефекта удается при размыкании цепи обратной связи.