Логико-вероятностная модель процесса отработки.

В настоящее время при создании новых образцов техники различают периоды разработки, производства и эксплуатации (см. рис. 1.1). Первые два периода объединяются понятием "создание системы объекта" (например, создание системы летательного аппарата). Процесс разработки состоит из ряда этапов: формирование тактико-технического задания (ТТЗ), эскизного проектирования, наземной и летательной отработки. Часто первые два этапа называют периодом проектирования объекта, а последние два – опытной отработкой [1-5].

Отработкой называется процесс внесения доработок.

Доработкой называется внесение изменений в конструкцию объекта или технологию его производства, при любых отклонениях объекта от требований конструкторской при эксплуатационной документации при испытаниях после наступления отказа с целью ликвидации причин их возникновения.

Отработка объектов происходит и осуществляется в процессе испытаний.

Испытания – экспериментальное определение количественных и (или) качественных характеристик свойств объекта испытаний как результата воздействия на него при его функционировании, при моделировании объекта и (или) воздействий [10]. Составной частью испытания является технический контроль.

Технический контроль(контроль) – проверка соответствия объекта установленным техническим требованиям [9].

Испытания на надежность – испытания, проводимые для определения показателей надежности в заданных условиях.

Таким образом, по смыслу причина отказа или любого отклонения от требований нормативно-технической или конструкторской документации устраняется проведением доработки конструкции, электрической схемы объекта, технологии производства и ремонта, эксплуатационной документации и программно-математического обеспечения. Поэтому после успешного проведения доработки устраняемый ею отказ или указание выше отклонения уже не возникает, что особенно характерно для программных продуктов.

Процесс внесения доработок (процесс отработки), обеспечивающий рост показателя надежности (безотказности) сложных объектов является аналогом различных моделей обучения. В частности, хорошо известна модель обучения мыши в Т-образном лабиринте (так называемая мышь Шеннона) [12-15]. При этой модели возникает задача количественной оценки закрепления какой-либо реакции мыши при многократном повторении опытов, в ходе которых желаемое поведение стимулируется. В этом случае мышь пускают по Т-образному лабиринту, в котором мышь может пойти налево или направо. Если, например, в левой части лабиринта мышь получает корм, то постепенно от опыта к опыту вероятность выбора мышью левого направления будет возрастать. При этом возникает задача отыскания аналитической зависимости, характеризующей обучаемость, например, вероятность поворота мыши налево.

В формализованном виде такой процесс обучения напоминает ход испытаний объекта, который за счет доработок как бы "учится" высокой надежности. При этом предполагается, что рост надежности (безотказности) объекта при испытаниях есть бесконечный процесс, в ходе которого показатель безотказности объекта стремится к единице 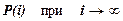, где i – номер испытания.

Пусть P(i) есть вероятность успешного проведения доработки или вероятность правильного ответа при единичном i-м испытании. Тогда вероятность того, что при проведенииq i-го испытания доработка не будет успешной или вероятность неправильного ответа (при обучении) составит q(i)=1-P(i). В общем случае каждая доработка увеличивает, уменьшает или оставляет неизменно надежность, так как причина отказов и меры их устранения в силу воздействия большого числа опытных факторов устанавливаются недостоверно. В общем случае предполагается деление результата доработки на две части: эффективную и негативную. Поэтому после испытания могут быть два исхода: проведение или отсутствие доработки. Соответственно приращения надежности за счет доработок после успешного испытания или после отказа будут неодинаковы. Все это обусловливает ветвящуюся структуру процесса отработки.

Если доработки объекта проводятся в конце каждого испытания и закон этой доработки известен, то

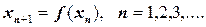(12.37)

где x – показатель или параметр характеризующей работоспособность объекта. При этом испытания нумеруются числами 0, 1, 2, ….

Таким образом, рост показателя надёжности при проведении доработок определяется наличием у испытателей и разработчиков информации о виде зависимости (12.37).

Пусть 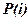есть вероятность успеха испытания (правильного ответа при испытании). В этом случае при реализации процесса (12.37) вероятность 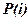непрерывно возрастает. Тогда вероятность q(i)=1-P(i) есть вероятность отказа при испытании с номером i. Эта вероятность непрерывно убывает.

Процесс отработки (12.37) является рекуррентным, поэтому из произвольного события этого процесса можно выделить исход (успех или отказ) и следствие (проведение или отсутствие доработки). Такое деление можно рассматривать как логическую основу этого процесса. Поэтому после любого испытания могут быть два несовместимых следствия: проведение или отсутствие доработки. Соответственно и приращения надёжности за счёт доработок после успеха или после отказа в общем случае неодинаковы и образуют ветвящийся процесс.

Для того, чтобы построить зависимости изменения надежности (безотказности) объекта от доработок необходимо создать модель роста надежности. В настоящее время получили распространение линейные модели роста надежности, поскольку они достаточно просты и имеют ясное логическое обоснование [1-5].

В линейных моделях предполагается, что с каждым новым испытанием вероятности 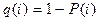убывают, причем коэффициент убывания остается постоянным для всех испытаний. Это означает существование такой константы 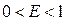, что зависимость (12.37) принимает вид

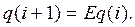(12.38)

Постоянная E называется первым параметром модели и характеризует скорость снижения ненадежности и роста надежности. Согласно прогнозу из модели (12.2) следует

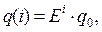(12.39)

откуда при i=0 q(0)=q₀. Величина q₀ является вторым параметром модели.

Параметры E и q₀ характеризуют случайный процесс изменения (роста) надежности при доработках, то есть процесс отработки объекта.

Линейные модели (12.37), (12.38) учитывают как возможность повышения, так и снижения достигнутой надежности, а также тот факт, что с ростом надежности ее повышение становится более трудным. Эти модели просты и дают ясное логическое обоснование. Линейные зависимости (12.37), (12.38) приводят к нелинейному изменению функции P(i), поскольку с увеличением P(i) ее приращения 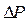существенно уменьшаются.

При отработке объектов высших уровней (см. рис.1.1) в каждом испытании при отработке участвует, как правило, один образец. Это приводит к тому, что изменение надежности объекта в ходе отработки отражается одной реализацией случайного ветвящегося процесса. Если отработка проведена и нужно оценить ее ход, то используется модель, отражающая реализацию процесса P(i), а если необходимо прогнозировать ход процесса отработки, то удобнее всего использовать модель его математического ожидания M[P(i)].

Математически рассмотренная линейная модель может быть описана следующим образом. Так, из рекуррентного соотношения (12.37) следует

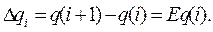(12.40)

Выражение (12.4) есть линейное неоднородное уравнение первого порядка в конечных разностях. Оно характеризует динамику отработки объекта в процессе испытаний. Непрерывным аналогом этого уравнения является дифференциальное уравнение:

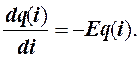(12.41)

Знак «минус» в правой части выражения (12.41) свидетельствует о снижении надежности объекта в ходе отработки.

Интегрирование выражения (12.41) приводит к следующему результату:

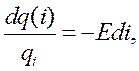(12.42)

откуда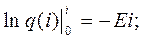

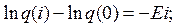
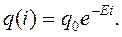(12.43)

Использование выражений 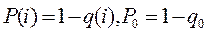позволяет перейти от уравнения снижения ненадежности (вероятности отказа) к уравнению роста надежности объекта при отработке. Тогда из уравнения (12.43) следует

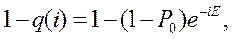
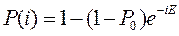. (12.44)

Полученное уравнение (12.44) является уравнением отработки объекта с учетом того, что доработки проводятся при каждом испытании, а в ходе отработки происходит устранение одной причины отказа. Однако доработки проводятся не после каждого испытания и определенным образом располагаются по числовой оси i.

Пусть при проведении n испытаний было равномерно выполнено 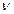отработок. В этом случае номер доработки i связан с номеромиспытания j формулой:

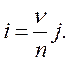(12.45)

Подобная линейная зависимость i(j) позволяет свести модель (12.44) к выражению

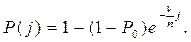(12.46)

Использование формулы (12.46) означает, что частота устранения причин отказов доработками определяется отношением 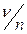и является аналогом вероятности E, характеризующей вероятность E успешного проведения доработки. Тогда выражение (12.46) может быть записано в виде

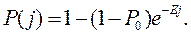(12.47)