Последовательный метод контроля надёжности.
Последовательный метод контроля не предусматривает предварительного определения объёма выборки. Задаются два уровня надёжности D0 и D1 и риски α и β. Информация о надёжности испытываемых изделий накапливается при последовательно возрастающем объёме испытаний m=n1+n2+…+nm определяется отношение правдоподобия γm и сравнивается с заранее определёнными оценочными нормативами A=(1- β)/ α; B= β/(1- α). Эти нормативы определяются на основании статистической теории оценивания. Отношение правдоподобия 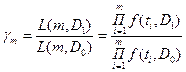 . Если
. Если 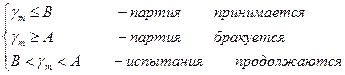
При последовательном контроле возможны два способа контроля:
- контроль числа дефектных изделий;
- контроль по наработке.
Рассмотрим эти виды контроля.
1. Контроль числа дефектных изделий.
Если контролируется малосерийная партия объёмом N<150 и dm- число дефектных изделий в выборке объёма “m”, то γm определяется с использованием гипергеометрического распределения:
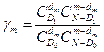 . (12.26)
. (12.26)
Здесь D0 – число дефектных изделий в партии хорошей надежности, D1 – число дефектных изделий в партии плохой надёжности (D0 и D1 задаются).
Формула (12.26) приводит к сложным расчетам. Более удобной и достаточно точной является формула, использующая 𝜑 – биномиальное распределение:
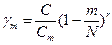 , (12.27)
, (12.27)
где 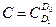 ;
; 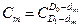 ;
; 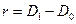 .
.
Для облегчения процедуры контроля можно заранее подсчитать для определённых значений dm=0,1,2,3… приёмочные (mпр) и браковочные (mбр) объёма испытаний:
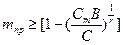 (12.28)
(12.28)
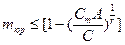 (12.29)
(12.29)
Рассчитанный таким образом план контроля может быть представлен в табличной или графической форме. На рис.12.8. показан график контроля, где область “П”, лежащая выше линии 1, - область приёмки, область “Б”, лежащая выше линии 2, - область браковки, область “ПИ”, заключённая между линиями 1,2 и осями координат, - область продолжения испытаний.
|
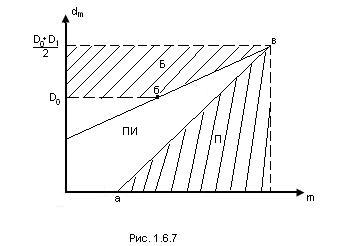
Графики контроля можно строить по трём точкам:
а) dm=0, 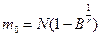 ;
;
б) dm=D0, 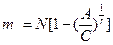 ;
;
в) 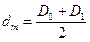 , m=N
, m=N
Для контроля больших партий изделий (N≥1000), а также восстанавливаемых изделий целесообразно пользоваться биномиальными планами. В этом случае
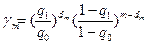 , (12.30)
, (12.30)
где q0 – вероятность отказа в каждом одиночном испытании для партии с хорошей надёжностью; q1 – то же для партии с плохой надёжностью. Из (12.30) вытекают формулы для приёмочных (dпр) и браковочных (dбр).
Имея дефектных испытаний из числа “m” испытаний
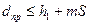 ,
, 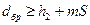 , (12.31)
, (12.31)
где 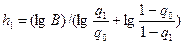 ,
, 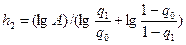 ,
, 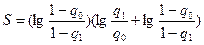
Приёмочные и браковочные числа для ряда значений “m” могут быть подсчитаны заранее и представлены виде таблиц плана. Для практических целей удобнее представлять план контроля в виде графика (Рис.1.2.8). Из (12.31) следует, что приёмочные (dпр) и браковочные (dбр) числа линейно зависят от объёма испытаний.
|
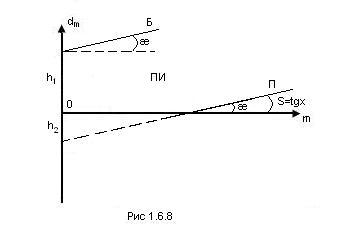
Если риски поставщика и заказчика равны: α=β, то h1=h2. Из (12.31) можно определить минимальное число испытаний m0, при котором можно принять партию, когда число отказов d=0: m0=-(h1/S).
Если контролируется надёжность большой партии изделий (N≥1000) или восстанавливаемых изделий при условии q1≤0,1, то исходя из распределения Пуассона, имеем:
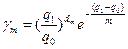 . (12.32)
. (12.32)
Тогда исходные величины для построения графика контроля определяются соотношениями:
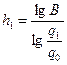 ;
; 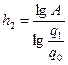 ;
; 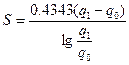 . (12.33)
. (12.33)
Все остальные положения последовательного контроля остаются такими же как и к биномиальном плане.
Контроль по наработке.
Рассмотрим случай экспоненциального распределения времени безотказной работы. В этом случае последовательный контроль надёжности по наработке осуществляется в соответствии с правилами:
Если
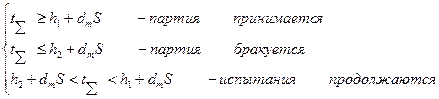 (12.34)
(12.34)
где 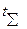 - суммарная наработка всех испытываемых изделий
- суммарная наработка всех испытываемых изделий
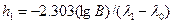 ;
; 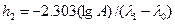 ;
;
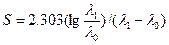 (12.35)
(12.35)
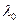 - интенсивность отказов изделий надёжной партии,
- интенсивность отказов изделий надёжной партии, 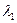 - то же ненадёжной партии.
- то же ненадёжной партии. 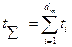 , (
, ( 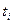 - наработка до отказа i-го изделия) – суммарная наработка на каждом этапе при неусечённых последовательных испытаниях невосстанавливаемых изделий. При одновременном испытании N невосстанавливаемых изделий на каждом этапе испытаний, отмеченных временем
- наработка до отказа i-го изделия) – суммарная наработка на каждом этапе при неусечённых последовательных испытаниях невосстанавливаемых изделий. При одновременном испытании N невосстанавливаемых изделий на каждом этапе испытаний, отмеченных временем 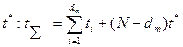 . Если на испытании находится N восстанавливаемых изделий, замена которых осуществляется практически мгновенно, то на каждом этапе:
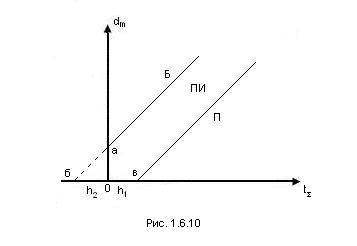
. Если на испытании находится N восстанавливаемых изделий, замена которых осуществляется практически мгновенно, то на каждом этапе: 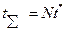 . График последовательного контроля изображён на рис 12.10.
. График последовательного контроля изображён на рис 12.10.
|
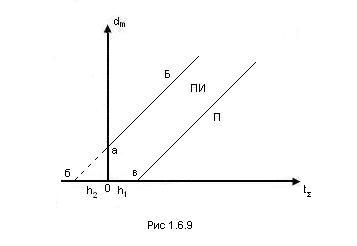
Характерными точками графика являются:
a) 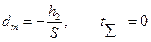 ;
;
б) 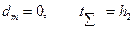 ;
;
в) 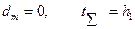
В случае нормального распределения с известной дисперсией последовательный контроль надёжности по наработке осуществляется в соответствии с правилами:
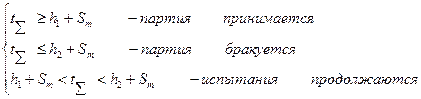 (12.36)
(12.36)
где 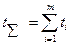 ;
; 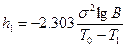 ;
; 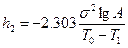 ;
; 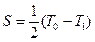 ,
, 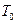 - средняя наработка в партии с хорошей надёжностью,
- средняя наработка в партии с хорошей надёжностью, 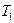 - то же в партии с плохой надёжностью.
- то же в партии с плохой надёжностью.
График последовательного контроля изображён на рис 12.11.
|
Характерными точками графика являются:
a) 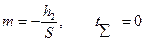 ;
;
б) 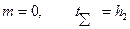 ;
;
в) 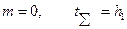
Типовые примеры решения задач последовательного контроля.
Пример № 1.
Последовательному контролю подлежит партия из N=100 невосстанавливаемых изделий. Партия считается хорошей при числе дефектных изделий q0=0,05 и плохой при q1=0,1. Риски поставщика и заказчика α=β=0,1. Определить приёмочные (mпр) и браковочные (mбр) числа испытаний при числе дефектных изделий dm=0,1,2,3,4,2. Построить график контроля и принять решение в случае dm=4 при числе испытаний m=22.
Решение: так как объём партии мал, используем f-биномиальный план.
1. Определяем число дефектных изделий в партии хорошей и плохой надёжности: D0=q0N=0,05*100=5; D1=q1N=0,1*100=10
2. Находим значения оценочных нормативов:
3. А=(1-β)/α=(1-0,1)/0,1=9; B=B/(1- α)=0,1/(1-0,1)=0,11.
4. Определяем С и r: 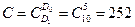 ; r=D1-D0=10-5=5;
; r=D1-D0=10-5=5;
Определяем приёмочные числа d=0,1,2…
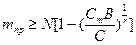
d=0: 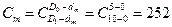 ;
; 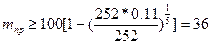 ;
;
d1=1: 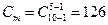 ;
; 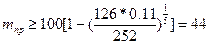 ;
;
и т.д.
5. Определяем браковочные числа:
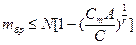 . Очевидно, эта формула имеет смысл при Сm<C/A=252/9=28.8, что в соответствии с таблицей биномиальных коэффициентов [22] имеет место при dm≥3. Для dm=3;
. Очевидно, эта формула имеет смысл при Сm<C/A=252/9=28.8, что в соответствии с таблицей биномиальных коэффициентов [22] имеет место при dm≥3. Для dm=3; 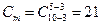 ;
; 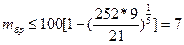 и т.д.
и т.д.
После расчета всех приёмочных и браковочных чисел таблица плана может быть представлена в виде:
Таблица 12.3. Таблица приёмочных и браковочных чисел плана
| dm | ||||||
| mпр не менее | ||||||
| mбр не более | - | - | - |
6. Определяются характерные точки графика плана:
а) dm=0; 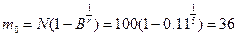 ;
;
б) dm=D0=5; 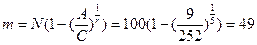 ;
;
в) 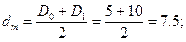 m=N=100.
m=N=100.
|
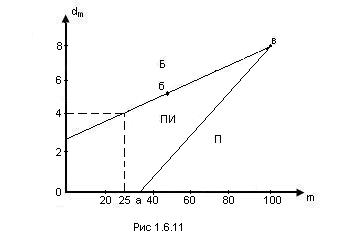
Заданная по условию рабочая точка попадает в область Б.
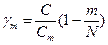 ; m=25; dm=4;
; m=25; dm=4; 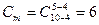 ; C=252;
; C=252; 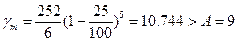 .
.
Т.е. партия бракуется.
Пример № 2.
Надёжность изделий, выпускаемых большой серией считается высокой при интенсивности отказов 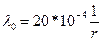 и низкой при
и низкой при 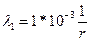 . Риски поставщика и заказчика одинаковы α=β=0,02. Рассчитывать последовательный план выходного контроля контроля до dm=m=10. Принять решение для 3х рабочих точек: d=0,
. Риски поставщика и заказчика одинаковы α=β=0,02. Рассчитывать последовательный план выходного контроля контроля до dm=m=10. Принять решение для 3х рабочих точек: d=0, 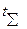 =5000ч.; d=1;
=5000ч.; d=1; 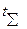 =5000ч.; d=2;
=5000ч.; d=2; 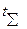 =300ч.
=300ч.
Решение:
1. Вычисляем значения оценочных нормативов:
А=(1-β)/α=(1-0,05)/0,05=19; B=B/(1- α)=0,05/(1-0,05)=0,053.
2. Вычисляем константы:
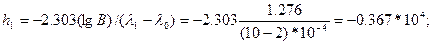
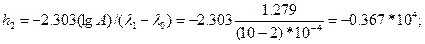
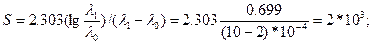
3. Таблицу плана вычисляем по формулам:
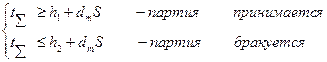
| dm | |||||||||||
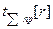 не менее не менее
| |||||||||||
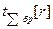 не более не более
| - | - |
4. График плана (Рис.12.13) можно построить с помощью полученной таблицы или по трём характерным точкам.
а) 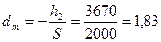 ;
; 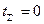
б) 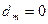 ;
; 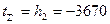
в) 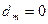 ;
; 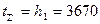
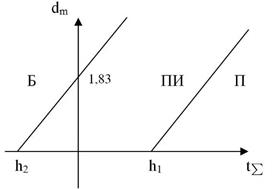
Рис. 12.15
Из графика рис. 12.13 видно:
1. Рабочей точке 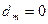 ,
, 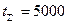 соответствует решение о приемке партии.
соответствует решение о приемке партии.
2. Рабочей точке 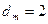 ,
, 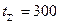 - решение о браковке.
- решение о браковке.
3. Рабочей точке 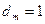 ,
, 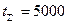 - решение о продолжении испытаний.
- решение о продолжении испытаний.
Дата добавления: 2016-09-26; просмотров: 4488;











