Контроль по методу однократной выборки.
Метод однократной выборки заключается в том, что из контролируемой партии объёма N изделий берётся одна случайная выборка объёма “n” изделий. Заданы риски α, β. Исходя из N, n, α, β устанавливаются оценочные нормативы А0 и А1. Если контролируется число дефектных изделий “d” в выборке “n”, то при d(n)≤ А0 – приём; d(n)≥ А1 – браковка.
Надёжность партии считается высокой, если в партии объёма N имеется D0 дефектных изделий (q0=D0/N) и низкой при наличии D1 дефектных изделий (q1=D1/N). При заданных α и β оценочные нормативы определяются из соотношений, использующих гипергеометрическое распределение (см. 1.4.2)
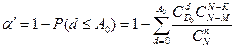 ;
;
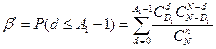 , (12.21)
, (12.21)
где 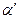 - риск поставщика, близкий к заданному α;
- риск поставщика, близкий к заданному α;
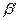 - риск заказчика, близкий к заданному β.
- риск заказчика, близкий к заданному β.
В общем случае 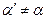 и
и 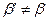 из-за дискретности гипергеометрического распределения. Практическое использование формул (12.21) при n>100 весьма затруднительно. При q0<0.1 и q1<0.1 хорошее приближение к (12.21) дают формулы:
из-за дискретности гипергеометрического распределения. Практическое использование формул (12.21) при n>100 весьма затруднительно. При q0<0.1 и q1<0.1 хорошее приближение к (12.21) дают формулы:
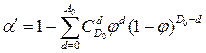
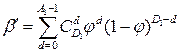 , (12.22)
, (12.22)
где 𝜑=n/N – оценка плотности биномиального распределения.
Соотношения (12.22) целесообразно использовать при N≤500. Когда объём партии N>500, а также при испытаниях восстанавливаемых изделий или когда n≤0.1N можно использовать следующие формулы:
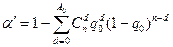
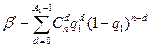 , (12.23)
, (12.23)
где q0 и q1 – вероятности отказа.
Для подсчёта А0 и А1 при n≤500 можно пользоваться табл. П 7.11 [22]. Если соблюдаются условия n≤0.1N; q0<0.1; q1<0.1 то можно использовать распределение Пуассона:
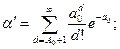
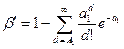 , (12.24)
, (12.24)
где a0=q0n; a1=q1n. Ошибка, возникающая при замене биномиального распределения распределением Пуассона имеет порядок q2n. Формулы (12.24) целесообразно использовать для контроля надёжности крупносерийных (n≥50) высоконадёжных устройств. Очень удобной таблицей для построения планов контроля, основанных на распределение Пуассона является таблица П.7.12 [22] , с помощью которой при заданных α иди β и А0 или А1 можно определить a0=nq0 или a1=nq1. При этом легко определить объём выборки, если известны q0 и q1, а также решить обратную задачу – найти q0 или q1, при заданном n.
Ниже приводиться фрагмент данной таблицы:
Таблица 12.2. Значения a=nq для заданных вероятностей распределения Пуассона
| A0 | A1 | α | |||||
| 0.01 | 0.05 | 0.10 | 0.90 | 0.95 | 0.99 | ||
| β | |||||||
| 0.99 | 0.95 | 0.90 | 0.10 | 0.05 | 0.01 | ||
| 0.01005 | 0.05129 | 0.10536 | 2.3026 | 2.9957 | 4.6052 | ||
| … | … | … | … | … | … | ||
| … | … | … | … | … | … | ||
| … | … | … | … | … | … | ||
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| 7.4768 | 9.2463 | 10.300 | 21.128 | 21.886 | 22.446 |
При контроле больших партий (50≤n≤0.1N) со сравнительно невысокой надёжностью (nq0≥4) можно пользоваться приближёнными формулами:
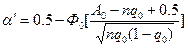 ;
;
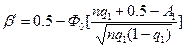 , (12.25)
, (12.25)
где Ф0 – функция Лапласа 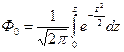 .
.
Ниже приводяться типовые примеры решения задач при одиночном контроле:
Пример №1.
Партия изделий состоит из N=50 экземпляров. Партия считается хорошей, если в ней содержится не более 10% дефектных изделий, и плохой – при содержании 20% дефектных изделий. Риски поставщика и заказчика: α=β=0,1. Определить приемлемое А0 и браковочное А1 числа дефектных изделий в выборке объёмом n=20.
Решение.
Так как N<100, а относительный объём выборки велик (n/N=0,4), то используем гипергеометрическое распределение (12.21).
1. Число дефектных изделий при 10% дефектных изделий в партии: D0=Nq0=50*0,1=5; при 20% дефектных изделий D1=Nq1=50*0,2=10.
2. Определяем числа А0 и А1. Для этого по формулам (12.21) накапливаем вероятности P до тех пор, пока накопленные вероятности не приблизятся к 1-α=P(d≤A0) и к β=P(d<A1-1).
Имеем: P(d≤A0)=1-α=1-0,1=0,90; Величины сочетаний (биномиальные коэффициенты) определяем по таблице П. 7.10 [22]. Далее получаем:
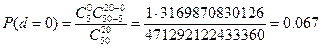 ;
;
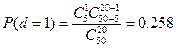 ;
;
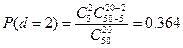 ;
;
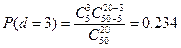 ;
;
P(d≤3)=0,067+0,258+0,364+0,234=0,923.
Полученная величина близка к 1-α=0,90, т.е. фактический риск поставщика близок к принятому: 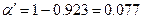 . Поэтому A0=3. Аналогичным образом рассчитываем поправочное число A1:
. Поэтому A0=3. Аналогичным образом рассчитываем поправочное число A1:
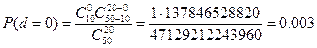 ;
;
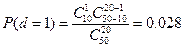 ;
;
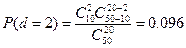 ;
;
P(d≤2)=0,003+0,028+0,096=0,127.
Следовательно с риском 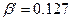 , близким к первоначальному установленному β=0,1 при d1=2 дефектных изделий в выборке партию можно принять, а при d1=3 – браковать (β=P(d1≤A1-1), A1=d1+1=2+1=3).
, близким к первоначальному установленному β=0,1 при d1=2 дефектных изделий в выборке партию можно принять, а при d1=3 – браковать (β=P(d1≤A1-1), A1=d1+1=2+1=3).
В данном случае А0=А1=3. Это означает, что одиночный контроль не может производится одновременно в интересах поставщика и заказчика. Защита интересов потребителя может привести к требованию браковочного числа, меньшего, чем приёмочное число при контроле в интересах поставщика. Обоюдно малый риск при браковочном числе, на единицу превышающем приёмочное, может быть получен в том случае, когда D1 существенно больше D0.
Пример № 2.
Контролю надёжности подлежит партия N=200 изделий. Определить приёмочное А0 и браковочное А1 числа дефектных изделий в выборке их n=40 изделий. Партия считается хорошей, если в ней содержится 5% и плохой – если 10% дефектных изделий. Риск поставщика α=0,20; риск заказчика β=0,1.
Решение.
Учитывая относительно большой объём контролируемой партии и небольшие значения доли дефектных изделий. Целесообразно производить решение, исходя из f-биномиального распределения, в соответствии с формулами (12.22)
1. Рассчитываем величины f, D0, D1:
f=n/N=40/200=0,2; D0=Nq0=10; D1=Nq1=20;
2. Определяем числа A0 и А1 суммированием вероятностей f-биномиального распределения до величин, близких к α и β.
Имеем: P(d≤A0)=1-α=1-0,2=0,8;
Вычисляем вероятности P(d) и суммируем их:
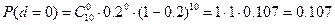 ;
;
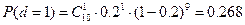 ;
;
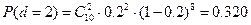 ;
;
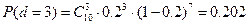 ;
;
P(d≤2)=0,107+0,268+0,320=0,695;
P(d≤3)=0,107+0,268+0,320+0,202=0,897.
Таким образом можно принять приёмочное число А0=2 с риском поставщика 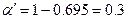 или А0=3 с риском поставщика
или А0=3 с риском поставщика 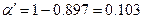 . Если требуется фактический риск приблизить к заданному, то это можно сделать при постоянных объеме партии и доле дефектных изделий в ней, варьируя объёмами выборки и приёмочными числами. Аналогичным образом рассчитываем браковочное число А1:
. Если требуется фактический риск приблизить к заданному, то это можно сделать при постоянных объеме партии и доле дефектных изделий в ней, варьируя объёмами выборки и приёмочными числами. Аналогичным образом рассчитываем браковочное число А1:
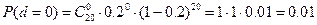 ;
;
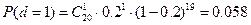 ;
;
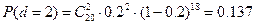 ;
;
P(d≤1)=0,01+0,058=0,068;
P(d≤2)=0,01+0,058+0,137=0,202.
Таким образом, целесообразно считать браковочным числом А1=2, тогда риск заказчика будет более близким к установленному.
Пример № 3.
С целью контроля надёжности проведены испытания 20 (n=20) восстанавливаемых объектов, при этом зарегистрировано 2 отказа (d=2). Необходимо решить, принять партию или забраковать, если контроль производится в интересах заказчика. Партия считается плохой, если q1≥0,1 (вероятность отказа). Решение должно быть принято с риском β=0,08.
Решение.
Исходя из условия задачи, контроль может быть произведён по биномиальному плану с помощью 2-ой из формул (1.2.23). Процедура решения сводится к накапливанию вероятностей до тех пор, пока кумулятивная вероятность станет близкой к заданному риску β. Сравнение числа отказов “d”, полученных при испытании с вычисленным браковочным числом А1 позволит принять решение:
Если d< А1, то партия принимается,
Если d≥ А1, то партия бракуется.
Используя таблицу П7.11 [22] определяющую вероятность “d” или меньшего количества дефектов изделий для биномиальных распределений, параметрами которой является n,q1,d находим, что для n=20, q1=0.1, d=2 находим 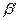 =0.68, что значительно превышает заданный риск. Из этой же таблицы видно, что при n=20, q1=0.1, d=0 вероятность составляет 0.12. Значит, принимая партию при d=0, риск
=0.68, что значительно превышает заданный риск. Из этой же таблицы видно, что при n=20, q1=0.1, d=0 вероятность составляет 0.12. Значит, принимая партию при d=0, риск 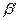 приёмки плохой партии будет равен 0.12.
приёмки плохой партии будет равен 0.12.
Пример № 4.
Из неограниченно большой партии изделий извлечена выборка объёмом n=50 изделий, которая испытана с целью контроля надёжности в интересах поставщика. Партия может быть принята с риском α=0.15, если вероятность отказа каждого изделия составляет q0=0.02. Определить приёмочное число А0.
Решение.
Так как партия неограниченно большая, то испытания независимы, это позволяет использовать биномиальный закон распределения и определять А0 по 1-ой из формул (12.23) или табл. П7.11 [22]:
Используя таблицу, при n=50, q0 =q1=0.05 вероятность 3 или меньшего количества изделий (d≤3) составляет 0.76, а для d≤4 – 0.90. Следовательно, приёмочное число можно взять А0=3, при этом риск поставщика составит 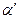 =1-0,76=0,24, или взять А0=4, тогда
=1-0,76=0,24, или взять А0=4, тогда 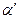 =1-0,9=0,1.
=1-0,9=0,1.
Пример № 2.
Установлены следующие параметры плана контроля. Приёмочное число А0=0, риск поставщика α=0,1 и вероятность безотказной работы q0=0,01.
Определить объём выборки, потребной для осуществления контроля по плану, основанному на распределении Пуассона.
Решение: используем формулы (12.24) или табл. П7.11 [20] для А0=0 и α=0,1 находим a=0,10536; по формуле n=a/q и заданному q0 определим объем выборки n=0,10536/0,01=11 единиц.
Пример № 6.
Для контроля надёжности в интересах заказчика выделена выборка n=40 штук. Установлены значения β=0,05 и браковочное число А1=2. Определить верхнее значение вероятности отказа в случае приёмки партии при d=1.
Решение: используем формулы (12.24) или табл. П7.11 [22] для А1=0 и β=0,05 находим a=4,74; По полученному “a” и заданному “n” находим: q1=a/n=4,74/40=0,12.
Пример № 7.
Партия проверяется в интересах поставщика с допустимым риском α=0,1. Приемлемая вероятность отказа q0=0,12. В результате испытаний получено d=8 отказов. Требуется произвести контроль партии изделий, выборка из которой объёмом n=100 экземпляров составляет незначительную долю (n/N<0,1).
Решение: для определения пригодности партии можно использовать формулу (12.25), полученную исходя из нормального закона. Подсчитаем величину z, подставив в формулу (12.25) значения “d” вместо А0:
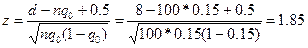
Определяем функцию Лапласа Ф0(1,85)=-0,468 (см. таблицу Ф(z)). По формуле (12.25) находим 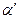 =0,5-Ф0(1,85)=0,5+0,468=0,968. Следовательно при А0=d=8 браковка партии приводит к риску поставщика
=0,5-Ф0(1,85)=0,5+0,468=0,968. Следовательно при А0=d=8 браковка партии приводит к риску поставщика 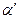 значительно превышающему заданный α=0,1. Для уменьшения риска нужно брать А0>>8. Нетрудно подсчитать, что А0=20 и при d=8 в данном примере партия может быть принята. (d(n)< А0).
значительно превышающему заданный α=0,1. Для уменьшения риска нужно брать А0>>8. Нетрудно подсчитать, что А0=20 и при d=8 в данном примере партия может быть принята. (d(n)< А0).
Дата добавления: 2016-09-26; просмотров: 4943;











