Интервальные оценки показателей надёжности.

В предыдущем параграфе были точечные оценки неизвестных параметров. Эти оценки являются случайными величинами. Какими бы хорошими свойствами эти оценки не обладали, например несмещённостью и эффективностью, все же в ряде случаев, представляющих большой практический интерес, оказывается недостаточным характеризовать качество и надёжность изделий только с помощью точечных оценок. Может оказаться, что при проведении испытаний отказы вообще не наблюдаются, а если и появляются, то в небольшом количестве. В результате величина оценок резко меняется от испытания к испытанию и не может служить устойчивой характеристикой надёжности изделий. Это приводит к выводу о целесообразности использования метода доверительных интервалов [2,18].

Р.Фишер в место функции θ(t₁…t_N) от результатов испытаний t₁…t_N, которая принимается за приближённое значение неизвестного параметра ищут две функции θ_н(t₁…t_N) и θ_в(t₁…t_N) от результатов испытаний, но не от самого параметра, для которых вероятность покрытия неизвестного параметра θ отрезком [θ_н, θ_в] равна заданной величине α:

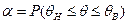, (12.15)

где α- двусторонняя доверительная вероятность,

θ_н, θ_в – доверительные границы,

[θ_н, θ_в] – доверительный интервал.

Часто возникает необходимость установить одну из границ интервала [θ_н, θ_в]: нижнюю θ_н или верхнюю θ_в, отвечающих доверительным вероятностям α₁ и α₂ – соответственно нижней и верхней доверительной вероятности.

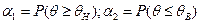. (12.16)

Величина β=1-α – вероятность того, что значение параметра θ выйдет из интервала [θ_н, θ_в] называется уровнем значимости.

Значение α обычно задаётся: α=0,90; α=0,95; α=0,99; Значение доверительного интервала [θ_н, θ_в] получают на основании информации о законе распределения времени до появления отказа. В самом общем случае определение доверительного интервала можно представить следующим образом. На рис. 12.2. показан произвольный закон распределения. [Т_н, Т_в] – доверительный интервал

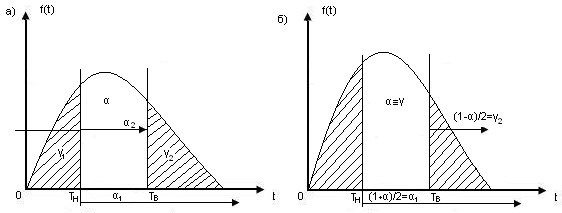
Рис. 12.8. Графическое представление доверительного интервала.

Из рисунка 12.6. а) видно, что α₁ + α₂ – γ = 1. Положение точки Т_н на оси t определятся α₁: 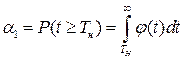. Положение Т_в – вероятностью α₂:

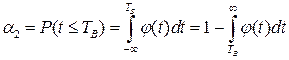(12.17)

Значения этих вероятностей следующим образом связаны с доверительной вероятностью α при условии, что доверительный интервал вписывается в середину площади, ограниченной кривой распределения:

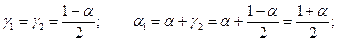
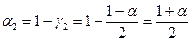(12.18)

Из рис. 12.6 также очевидно, что числовые значения границ доверительного интервала зависят не только от заданной доверительной вероятности, но и от закона распределения случайной величины (в данном случае величины τ – времени до появления отказа). В источниках [2,5,22] имеются таблицы, позволяющие на основании формул (12.17) определять доверительные интервалы для: 1) средней наработки на отказ T по зафиксированным временам возникновения отказов; 2) вероятности отказа в одном испытании по числу отказавших изделий. Рассмотрим эти задачи.