Метод максимального правдоподобия.
Этот метод состоит в том, что в качестве точечной оценки  параметра
параметра  принимается то значение параметра
принимается то значение параметра  , при котором функция правдоподобия достигает своего максимума.
, при котором функция правдоподобия достигает своего максимума.
Для случайной наработки до отказа с плотностью вероятности f(t,  ) функция правдоподобия определяется формулой 12.11:
) функция правдоподобия определяется формулой 12.11: 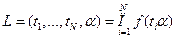 , т.е. представляет из себя совместную плотность вероятности независимых измерений случайной величины τ с плотностью вероятности f(t,
, т.е. представляет из себя совместную плотность вероятности независимых измерений случайной величины τ с плотностью вероятности f(t,  ).
).
Если случайная величина дискретна и принимает значения Z1,Z2…, соответственно с вероятностями P1(α),P2(α)…, 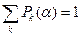 , то функция правдоподобия берётся в ином виде, а именно:
, то функция правдоподобия берётся в ином виде, а именно: 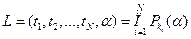 , где индексы у вероятностей показывают, что наблюдались значения
, где индексы у вероятностей показывают, что наблюдались значения 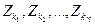 .
.
Оценки максимального правдоподобия параметра  определяются из уравнения правдоподобия
определяются из уравнения правдоподобия 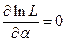 (12.12).
(12.12).
Значение метода максимального правдоподобия выясняется следующими двумя предположениями:
Если для параметра  существует эффективная оценка
существует эффективная оценка  , то уравнение правдоподобия (12.12) имеет единственное решение
, то уравнение правдоподобия (12.12) имеет единственное решение 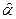 .
.
При некоторых общих условиях аналитического характера, наложенных на функции f(t,  ) решение уравнения правдоподобия сходится при
) решение уравнения правдоподобия сходится при 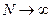 к истинному значению параметра
к истинному значению параметра  .
.
Рассмотрим пример использования метода максимального правдоподобия для параметров нормального распределения.
Пример:
Имеем: 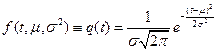 ,
, 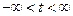 , ti (i=1..N) выборка из совокупности с плотностью распределения
, ti (i=1..N) выборка из совокупности с плотностью распределения 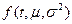 .
.
Требуется найти оценку 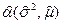 максимального подобия.
максимального подобия.
Функция правдоподобия: 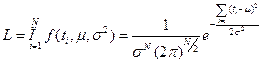 ;
;
 .
.
Уравнения правдоподобия: 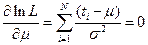 ;
;
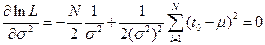 ;
;
Решение этих уравнений имеет вид: 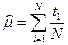 - статистическое среднее;
- статистическое среднее; 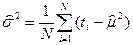 - статистическая дисперсия. Оценка
- статистическая дисперсия. Оценка 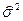 является смещённой. Не смещённой оценкой
является смещённой. Не смещённой оценкой 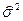 будет оценка:
будет оценка: 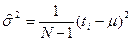 .
.
Основным недостатком метода максимального правдоподобия являются вычислительные трудности, возникающие при решение уравнений правдоподобия, которые, как правило, являются трансцендентными.
Метод моментов.
Этот метод предложен К.Пирсоном и является самым первым общим методом точечной оценки неизвестных параметров. Он до сих пор широко используется в практической статистике, поскольку нередко приводит к сравнительно несложной вычислительной процедуре. Идея этого метода состоит в том, что моменты распределения зависящие от неизвестных параметров, приравниваются к эмпирическим моментам. Взяв число моментов, равное числу неизвестных параметров, и составив соответствующие уравнения, мы получим необходимое число уравнений. Чаще всего вычисляются первые два статистических момента: выборочное среднее 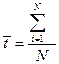 ; и выборочная дисперсия
; и выборочная дисперсия 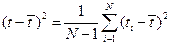 . Оценки, получаемые с помощью метода моментов, не являются наилучшими с точки зрения их эффективности. Однако очень часто они используются в качестве первых приближений.
. Оценки, получаемые с помощью метода моментов, не являются наилучшими с точки зрения их эффективности. Однако очень часто они используются в качестве первых приближений.
Рассмотрим пример использования метода моментов.
Пример: Рассмотрим экспоненциальное распределение:
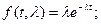 t>0; λ<0; ti (i=1..N) – выборка из совокупности с плотностью распределения
t>0; λ<0; ti (i=1..N) – выборка из совокупности с плотностью распределения 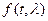 . Требуется найти оценку
. Требуется найти оценку 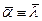 для параметра λ.
для параметра λ.
Составляем уравнение: 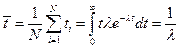 . Таким образом,
. Таким образом, 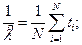 иначе
иначе 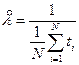 .
.
Метод квантилей.
Это такой же эмпирический метод, как и метод моментов. Он состоит в том, что квантиль теоретического распределения приравниваются к эмпирической квантили. Если оценке подлежат несколько параметров, то соответствующие равенства пишутся для нескольких квантилей.
Рассмотрим случай, когда закон распределения F(t,α,β) с двумя неизвестными параметрами α, β. Пусть функция F(t,α,β) имеет непрерывно дифференцируемую плотность 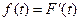 , принимающую положительные значения для любых возможных значений параметров α, β. Если испытания проводить по плану [N, U, r], r>>1, то момент
, принимающую положительные значения для любых возможных значений параметров α, β. Если испытания проводить по плану [N, U, r], r>>1, то момент 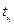 появления
появления 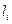 - го отказа можно рассматривать как эмпирическую квантиль уровня
- го отказа можно рассматривать как эмпирическую квантиль уровня 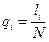 , i=1,2… ,
, i=1,2… , 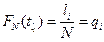 - эмпирическая функция распределения. Если бы tl и tr – моменты появления l-го и r-го отказов известны точно, значения параметров α и β можно было бы найти из уравнений
- эмпирическая функция распределения. Если бы tl и tr – моменты появления l-го и r-го отказов известны точно, значения параметров α и β можно было бы найти из уравнений
F(tl,α,β)= qe, F(tr,α,β)= qr (12.13)
Нам известны лишь приближённые значения квантилей qe и qr. Заменяя в уравнениях (12.13) значения квантилей их оценками, получаем уравнения 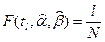 ,
, 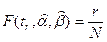 (12.14) (обычно
(12.14) (обычно 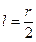 ). Решение
). Решение 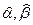 уравнений (12.14) являются состоятельными оценками для параметров
уравнений (12.14) являются состоятельными оценками для параметров 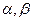 при
при 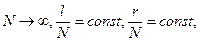 что непосредственно следует из непрерывности функции F(t,α,β). Можно показать, что эти оценки при весьма общих предположениях типа гладкости функции F(t,α,β) являются асимптотически несмещёнными и асимптотически нормально распределёнными.
что непосредственно следует из непрерывности функции F(t,α,β). Можно показать, что эти оценки при весьма общих предположениях типа гладкости функции F(t,α,β) являются асимптотически несмещёнными и асимптотически нормально распределёнными.
Проиллюстрируем метод квантилей на примере закона Вейбулла: 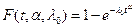 . Испытания проводятся по плану [N, U, r]. Выбираем значение
. Испытания проводятся по плану [N, U, r]. Выбираем значение 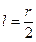 . В результате испытаний фиксируются значения tl и tr моментов l-го и r-го отказов. Уравнения (1.2.14) переписываются в виде:
. В результате испытаний фиксируются значения tl и tr моментов l-го и r-го отказов. Уравнения (1.2.14) переписываются в виде:  Разрешая их относительно неизвестных параметров
Разрешая их относительно неизвестных параметров 
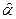 и
и 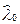 , получаем оценки:
, получаем оценки: 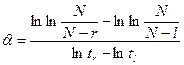 ;
;  .
.
Дата добавления: 2016-09-26; просмотров: 5892;











