Определение доверительного интервала для средней наработки на отказ
Используется то обстоятельство, что отношение удвоенного значения суммарной наработки на отказ к среднему времени безотказной работы имеет распределение χ2 , причём время отказа подчиняется экспоненциальному закону. Отсюда возникает возможность определять нижнее и верхнее значения Т, если задана доверительная вероятность α. Т.о. 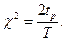 Из рис. 12.7 видно, что доверительная вероятность γ≡α, соответствующая заштрихованной площади, ограничена двумя значениями χ2: нижним значением, равным
Из рис. 12.7 видно, что доверительная вероятность γ≡α, соответствующая заштрихованной площади, ограничена двумя значениями χ2: нижним значением, равным 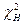 и верхним
и верхним 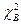 .
.
|
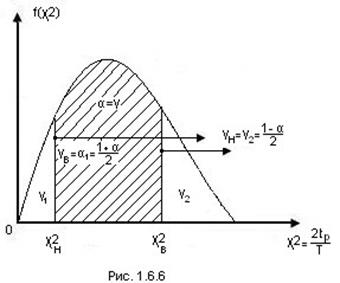
Поэтому нижнее значение Т при известных величинах – суммарной наработке tp и доверительной вероятности γ≡α будет равно:
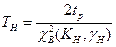 , где
, где 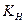 =2n+2 – число степеней χ2- распределения при определении ТH;
=2n+2 – число степеней χ2- распределения при определении ТH; 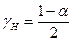 - значение вероятности того, что χ2 больше
- значение вероятности того, что χ2 больше 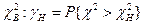 . Для определения
. Для определения 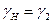 используется таблица квантилей распределения χ2 [Л..] Имеем:
используется таблица квантилей распределения χ2 [Л..] Имеем: 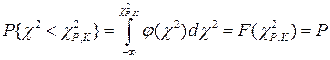 - квантиль уровня “P” распределения χ2.
- квантиль уровня “P” распределения χ2.
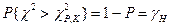
Верхнее значение Т при тех же параметрах равно 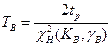 , где
, где 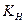 =2n – число степеней свободы χ2- распределения при определении Тв.
=2n – число степеней свободы χ2- распределения при определении Тв.
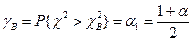 .
.
Таким образом, границы доверительного интервала для Т определяются выражением:
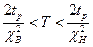 (12.19)
(12.19)
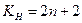 ;
; 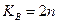 ;
; 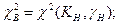
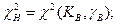
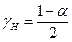 ;
; 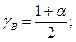
Среднее значение средней наработки на отказ равно 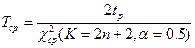
Рассмотрим пример:
Получены следующие результаты по плану [N,U,N]; n1,n2 – соответственно числа отказов, полученные при первом (N1=21) и втором (N2=10) испытаниях:
| tчас | ||||||||
| n1 | ||||||||
| n2 | - | - | - |
Определить доверительный интервал для Т с доверительной вероятности α=0.8, а также Тср.
Решение.
Для первого испытания:
tp=6*100+5*200+3*300+500+600+700+800+800=6300ч. 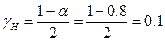 ; Kн=2n+2=2*21+2=44;
; Kн=2n+2=2*21+2=44; 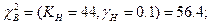
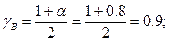 KB=2n=42;
KB=2n=42; 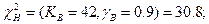
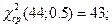
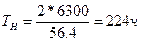 ;
; 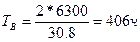 ;
; 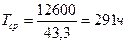 .
.
Для второго испытания: tp=100+2*200+4*300+2*400+500=3000ч.; Kн=2n+2=2*10+2=22; KB=2n=20; 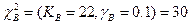 ;
; 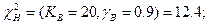
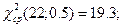
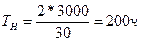 ;
; 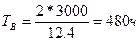 ;
; 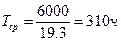 .
.
Для значений 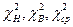 была использована таблица, построенная на основе квантилей
была использована таблица, построенная на основе квантилей 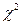 - распределения. В этой таблице K- число степеней свободы, γ- вероятность того, что
- распределения. В этой таблице K- число степеней свободы, γ- вероятность того, что 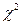 принимает значение, большее указанного в таблице. Приведём форму этой таблицы: Значения
принимает значение, большее указанного в таблице. Приведём форму этой таблицы: Значения 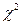 в зависимости от K и γ:
в зависимости от K и γ:
Таблица 12.1. Таблица 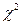 - рспределения
- рспределения
| K | γ |
| 0,99 … … … … … … … … … … … … … … 0,05 | |
| . . |
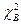 , , 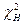
|
Определение доверительного интервала для вероятности отсутствия отказа в одном испытании по числу обнаруженных отказов.
Этот случай возникает при решении следующих типовых задач. По линии связи передается N команд; “n” команд не доходят до исполнителя за данное время. Требуется определить доверительный интервал для вероятности прохождения команд за данное время. Аналогичная задача возникает при испытании N изделий с целью определения вероятности отсутствия отказов за данное время.
Доверительный интервал определяется из следующих уравнений для вероятности того, что число отказов будет не меньше “n”. Эти уравнения записываются с использованием биноминального закона распределения, определяющего вероятность появления числа “n” события “A” в N независимых испытаниях (см. 12.2).
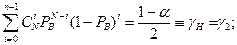
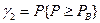 ;
;
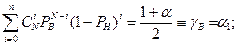
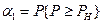 (12.20)
(12.20)
где 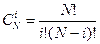 - число сочетаний из N по i, PB и PH – верхнее и нижнее значение вероятности отсутствия отказов в одном испытании.
- число сочетаний из N по i, PB и PH – верхнее и нижнее значение вероятности отсутствия отказов в одном испытании.
По уравнения (12.20) составлены таблицы [2,3,4,8,15,20], позволяющие определить нижнее и верхнее значения доверительного интервала для вероятности отсутствия отказа по заданным значениям N и n. Например, решается задача:
Определить доверительный интервал с вероятностью α=0,9 для вероятности отсутствия отказа изделия в одном испытании, если при испытаниях N=40 изделий отказало 12.
По таблице [Л прил.8] находим PH=0,6412; PB=0,8382.
Дата добавления: 2016-09-26; просмотров: 3758;











