Особенности расчёта надёжности резервированных восстанавливаемых систем.
Рассмотрим восстанавливаемую резервированную систему, в которой происходит восстановление отказавших элементов за счёт имеющегося резерва. Пусть в системе имеется: “n” – основных рабочих объектов,
m+l+S – резервных изделий, причём
m – число изделий в нагруженном резерве;
l- число изделий в облегчённом резерве;
S- число изделий в ненагруженном резерве;
z – объём ремонтного устройства.
Все рабочие изделия как и остальные одинаковы между собой по надёжности.
Поток отказов и восстановлений подчиняется экспоненциальному закону: λ=const, u=const.
Работа рассматриваемой системы иллюстрируется рис. 10.2:
|
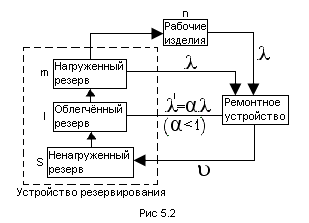
Каждое отказавшее рабочее изделие мгновенно поступает в ремонтное устройство и мгновенно замещается изделием из нагруженного резерва.
Каждое вышедшее из строя или перешедшее в основное рабочее состояние изделие из нагруженного резерва мгновенно замещается изделием из облегчённого резерва. Каждое отказавшее или перешедшее в нагруженный резерв изделие из облегчённого резерва, каждое восстановленное изделие поступает в ненагруженный резерв. Всего в системе имеется N=n+m+l+S изделий и она полностью выполняет свои функции, если число исправленных не меньше “n”. Система выходит из строя, если откажут m+l+S+1 изделий. (j=m+l+S). Используется метод, основанный на исследовании схемы состояний [2,4,5,15,18].
Под состоянием системы будем понимать число отказавших изделий: “K”
Граф состояний представлен на рис. 10.3:
|
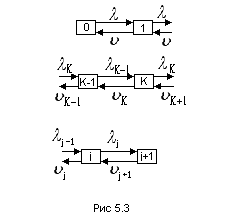
Параметры процесса отказов и восстановлений зависят от номера состояния “K”: λK, uK
Если 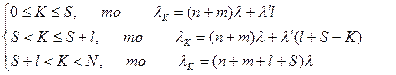 . (10.12)
. (10.12)
Если 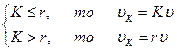 ,
, 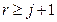 .
.
Описанная схема работы системы охвачивает большое число частных случаев. Мы рассмотрим два примера из множества возможных вариантов и определим финальные вероятности состояний. Исследование характеристик надёжности формируемых под воздействием потоков отказов и восстановлений, позволяет сделать вывод о том, что при существующих в практике соотношениях λ и u наступает сравнительно быстро период установившегося режима, т.е. можно положить 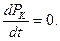 Тогда система дифференциальных уравнений Колмогорова трансформируется в систему алгебраических уравнений.
Тогда система дифференциальных уравнений Колмогорова трансформируется в систему алгебраических уравнений.
Если обозначить: ПК=-λКPК+uК+1PK+1, то для стационарного режима получим следующую систему:
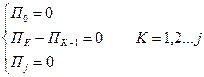 . (10.13)
. (10.13)
Из (10.13) Находим: ПК=0; k=0,1…j
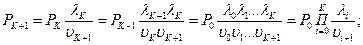 Вероятность P0 находим из условия нормировки
Вероятность P0 находим из условия нормировки 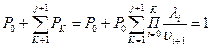 Pj+1=КП – коэффициент простоя, 1-Pj+1=Kr – коэффициент готовности.
Pj+1=КП – коэффициент простоя, 1-Pj+1=Kr – коэффициент готовности.
Частные случаи:
1. Полное число изделий в системе N. Из них “N-m” находятся в рабочем состоянии, а остальные составляют нагруженный резерв. Ремонтное устройство имеет объём r≥N (неограниченное восстановление).
Тогда λK=(N-K)λ; uK=Ku, где как было указано выше, “K” – число отказавших изделий (номер состояния).
Стационарная вероятность состояния “K” определяется по формуле:
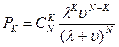
2. Система имеет “n” рабочих элементов и неограниченный ненагруженный резерв. Объем ремонтного устройства также неограничен. Для этого случая: λK=n λ ; uK=Ku;
Стационарная вероятность состояния “K” определяется по формуле:
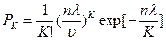
Дата добавления: 2016-09-26; просмотров: 2321;











