Оптимальное соотношение между надежностью и стоимостью

Создание высоконадежных объектов требует применения дорогостоящих материалов, увеличения времени на испытания, отработки специальных технологий изготовления, совершенствования методик контроля. Опыт показывает, что затраты на увеличение надежности растут тем быстрее, чем выше достигнуты уровень надежности.

В связи с этим представляет интерес определение условий при которых обеспечивается максимальное значение надежности (показателя надежности объекта) при заданных затратах на его создание и отработку.

На основании вышеизложенного может быть рассмотрен объект, состоящий, например, из трех элементов (таким элементами могут быть узлы, блоки, подсистемы и т. д.), а полученные выводы могут быть распространены на случай когда объект состоит из любого числа элементов. В этом случае общее выражение надежности объекта 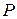, как функции стоимости трех его элементов 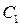, 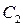и .

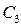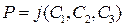. (11.1)

Ограничитель на условия состоит в том, что сума стоимости элементов должна быть равна заданной стоимости :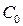

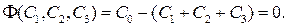(11.2)

Решая поставленную оптимизационную задачу методом неопределенных множителей ЛаГранжа, можно записать

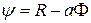, (11.3)

где 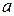- множитель Лагранжа.

На этой основе максимальное значение для функций надежности объекта (11.1) с учетом ограничений (11.2) может быть получено методом неопределенных множителей Лагранжа:

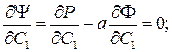(11.4)

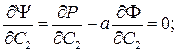(11.5)

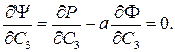(11.6)

Выражения (11.27) и (11.28) можно объединить следующим образом:

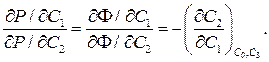(11.7)

Но поскольку из выражения (11.2) следует, что 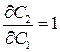, то формулу (11.7) можно представить в виде:

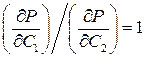. (11.8)

Аналогичным образом может быть получено выражение:

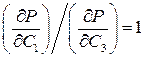(11.9)

и т.д.

Уравнения (11.8) и (11.9) есть необходимые и достаточные условия оптимального распределения стоимости элементов с целью получения максимальной надежности объекта.

В большинстве случаев надежность объекта выражается через соответствующие показатели его элементов следующим образом:

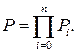(11.10)

В этом случае

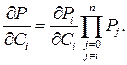(11.11)

Тогда необходимое условие оптимума с учетом выражения (11.8) приобретает вид:

. (11.12)

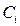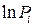В дальнейшем оптимальное значение стоимости определяется в зависимости от величины его надежности (показателя надежности ). Типичные кривые зависимости от 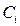приведены на рис.11.1.

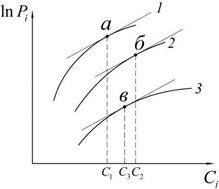
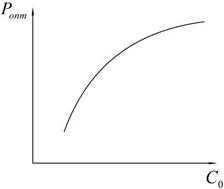
Рис. 11.1. Кривые соотношения Рис.11.2. Оптимальная надежность

надежность-стоимость для объекта, как функция полной

отдельных элементов объекта заданной стоимости

Порядок определения оптимальной надежности объекта на основе рис. 11.1. заключается в следующем. На кривой 1 выбирают, например, точку «а» и проводят в этой точке касательную к кривой 1. Затем на кривых 2 и 3 выделяют соответсвенно точки «б» и «в», в которых угол наклона касательных равен углу наклона касательной к кривой 1 в точке «а». Полная стоимость объекта будет равна сумме стоимостей отдельных элементов в точках «а», «б» и «в». Надежность объекта в целом определяется, как функция надежностей элементов по формуле (11.10). Эта надежность является максимально достижимой при заданной стоимости объекта 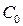и обозначается как .

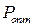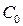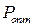Другие значения и могут быть получены путем выбора других углов наклона касательных. Кривая зависимости 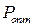от 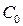приведена на рис. 11.2. Каждая ее точка представляет собой максимальную надежность при заданной полной стоимости объекта 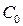или минимальную полную стоимость 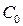при заданной надежности.

Описанный выше метод применяется последовательными шагами, начиная с отдельных элементов и кончая оптимизацией надежности объекта в целом. На начальных этапах (как это показано на рис. 1.1.) отдельными единицами могут быть комплектующие элементы, затем составляющие элементы, основные элементы и т.д.

Если ограничения типа (11.2) несколько или они заданны в виде неравенств, то решение поставленной задачи осуществляется методами математического программирования.