Определение надежности с учетом восстанавливаемости и числа запасных элементов

Рассмотрим систему многократного действия, которую можно представить в виде комплекса, состоящего из N однотипных по надежности элементов, имеющих интенсивность отказов, равную 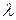. При допущении простейшего потока возникающих в аппаратуре отказов общая (суммарная) интенсивность отказов системы 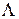определится по известной формуле .

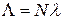Распределение плотности вероятности времени безотказной работы 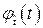имеет вид

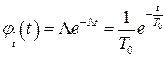. (10.14)

Известно также, что система должна выполнять заданные функции в течение длительного времени t (предполагаемый период эксплуатации).

За это время в системе может произойти случайное число отказов n, обусловленное ненадежностью отдельных ее элементов.

Предположим, что отказавший элемент не восстанавливается. Обычно при эксплуатации радиоэлектронной аппаратуры это допущение выполняется. При этом вместо отказавшегося элемента каждый раз из запаса будет изыматься новый элемент, поэтому число израсходованных элементов за это же время (без учета вторичных отказов).

При оговоренных условиях вероятность 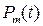того, что за время t система потребует точно 𝑚 запасных элементов (число замен), определится по формуле Пуассона

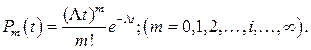(10.15)

Допустим, что в запасе нет ни одного элемента, т.е. 𝑚=0. Какова при этом будет вероятность 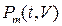выполнения системой своих задач?

Исходя из чисто физических предпосылок, можно сделать вывод о том, что вероятность того, что система не будет простаивать на заданном интервале t при 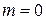есть не что иное, как вероятность безотказной работы за время 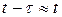(так как 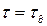– допустимое время простоя обычно много меньше времени эксплуатации t); следовательно,

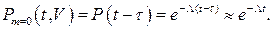(10.16)

Вероятность того, что система выполнит свои функции за время t с учетом восстанавливаемости и наличия 𝑚 запасных элементов, может быть определена по формуле [67]

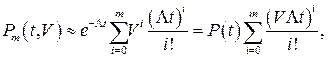(10.17)

где V=V( 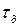) – вероятность восстановления системы за время .

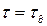Рассмотрим некоторые частные случаи приведенной формулы для вероятности .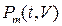

1. Число запасных элементов 𝑚=0, V≠0.

Из (10.18) имеем

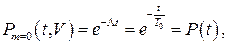
т.е. получаем известную формулу для вероятности исправной работы до первого отказа. Следовательно, если оперативное время работы системы достаточно велико ( 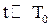), то при отсутствии запасных элементов вероятность выполнения системой своих функций весьма мала.

2. Число запасных элементов 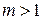, V≠0.

В этом случае 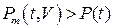, так как сумма

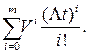
в формуле (10.18) всегда больше единицы.

При этом чем больше число 𝑚, тем больше вероятность 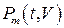по сравнению с .

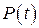Количественную оценку выигрыша работоспособности аппаратуры 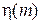, определяемого как отношение 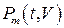к 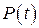, находим по формуле

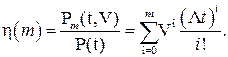(10.18)

Значения коэффициента выигрыша для 𝛬t=1и V=0.9 приведены в табл. 10.1.

Таблица 10.1

𝑚
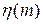
	1,9	2,3	2,4	2,45	2,46	2,5

Необходимо отметить, что величина коэффициента выигрыша в сильной степени зависит не только от объема запасных элементов, но и от значения вероятности восстановления V и времени эксплуатации t.

3. Число запасных элементов постоянно, т.е. 𝑚=const, а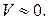

На практике такие случаи могут иметь место, если:

- допустимое время простоя мало, т.е. для аппаратуры не допускаются даже кратковременные перерывы в работе и требуется непрерывная безотказная работа;

- допустимое время простоя 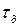намного меньше, чем среднее время восстановления;

- используется аппаратура однократного действия, для которой .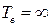

В этом случае из (10.18) имеем

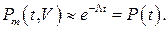
Таким образом, если восстанавливаемость очень низкая, то даже большой объем запасных элементов не даст выигрыша в безотказности системы, так как вероятность 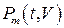практически равна вероятности безотказной работы.

Отсюда еще раз вытекает вывод о том, что наряду с требованием обеспечения высокой безотказности элементов аппаратуры большое внимание должно уделяться требованию высокой восстанавливаемости систем.

4. Число 𝑚=const, а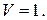

На практике такие случаи могут быть, если:

- рассматривается идеальная самовосстанавливающаяся система, у которой отказавший элемент автоматически и мгновенно заменяется новым;

- допустимое время простоя 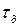намного больше, чем среднее время восстановления ;

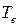-рассчитывается общий объем требуемого количества запасных элементов без учета параметров процесса восстановления.

Из формулы (10.18) при V=1 имеем

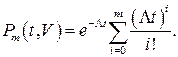(10.19)

Полученная вероятность может быть интерпретирована как вероятность того, что за время t система потребует меньше чем 𝑚 запасных элементов. С другой стороны, если задаться фиксированным значением числа 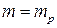, то вероятность 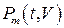может быть предложена в качестве критерия, гарантирующего с вероятностью 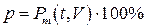уверенность в том, что система выполнит свои задачи.

Поэтому выражение (10.19) будет использовано при определении гарантированного числа запасных элементов 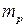для систем многократного действия.

5. Задана вероятность восстановления V, а 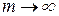(т.е. мы предполагаем, что для поддержания системы в работоспособном состоянии всегда имеются запасные элементы). Тогда из формулы (10.17) (при 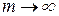) получаем выражение

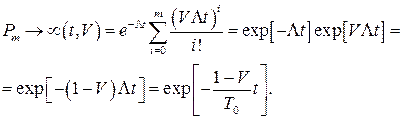
Мы опять пришли к выводу, что при достаточном числе запасных элементов параметр безотказности 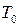с учетом восстанавливаемости должен определяться по формуле

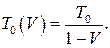
Таким образом, формула (10.17) дает нам количественную зависимость надежности систем многократного действия с учетом восстанавливаемости и числа запасных элементов.

Рассмотрим теперь задачу расчета потребного количества запасных элементов.