Вычисление функций готовности и простоя нерезервированных систем

Нерезервированная система может находиться в любой момент времени “t” в одном из двух состояний:

«0» - система работоспособна;

«1» - система неработоспособна и ремонтируется.

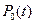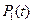Обозначим вероятности этих состояний: и . Очевидно 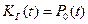; 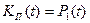. При длительной эксплуатации при 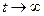получаем установившиеся значения , .

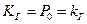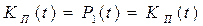Рассматриваем случай, когда время безотказной работы и время восстановления имеют экспоненциальное распределение: 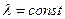, 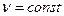. На рис. 10.1 приведен граф состояний системы.

Рис. 10.1

В соответствии со схемой рис. 10.1 запишем следующую систему дифференциальных уравнений Колмогорова.

; (10.4)

.

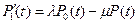Если при 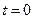система находилась в работоспособном состоянии, то P₀(0)=1; P₁(0)=0 и в результате решения уравнений 10.4 (например, с использованием преобразования Лапласа) получим:

,

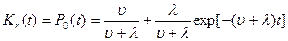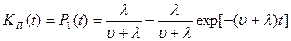. (10.5)

Если при t=0 система находилась в ремонте, то P₀(0)=0; P₁(0)=1 и решение системы (10.4) будут иметь вид:

,

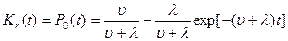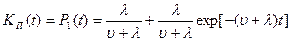. (10.6)

При 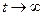получаем

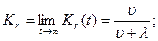
(10.7)

Так как 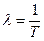и 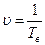[2,18], то можно записать:

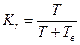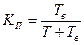; , (10.8)

т.е. (Т и Т_в соответственно среднее время безотказной работы и среднее время восстановления) коэффициент готовности характеризует долю времени, в течении которого система работоспособна, а коэффициент простоя – долю времени, в течении которого она ремонтируется.

Выражения для коэффициентов готовности и простоя можно определить непосредственно по графу переходов. Для этого используется следующее правило [2,4,18]: для определения стационарной вероятности P_k нахождения системы в “K”-ом состоянии необходимо идти по направлению стрелок из каждого крайнего состояния в “К”-е по кратчайшему пути и перемножить все интенсивности переходов, соответствующие проходимым стрелкам. Таким образом проходятся все пути из всех крайних состояний в каждое состояние системы. При разветвлённой схеме состояний некоторые участки пути придется проходить несколько раз. При этом интенсивности переходов этих участков нужно учитывать только один раз. Вероятность нахождения системы в “К”-ом состоянии

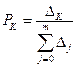, (10.9)

где 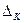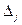- произведения интенсивностей переходов из всех крайних состояний соответственно в “К”-ое и “j”-ое при движении по кратчайшему пути в направлении стрелок; “m+1” – число состояний системы.

При нескольких работоспособных состояниях

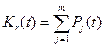, (10.10)

где “n”- число работоспособных состояний; 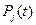- вероятность j-го работоспособного состояния.

Часто число неработоспособных состояний значительно меньше числа работоспособных. При этом удобнее вычислить функцию простоя:

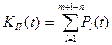, (10.11)

где P_l(t) –вероятность l-го неработоспособного состояния; “m+1” – общее число состояний.