Векторное произведение.

Определение.

Вектор 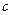называется векторным произведением векторов 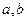, обозначается 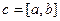, если выполнены 3 условия: 1) , .

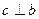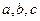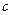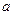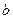2) Векторы образуют правоориентированную тройку, то есть с конца вектора кратчайший поворот от к виден против часовой стрелки.

3) 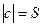параллелограмма, образованного парой векторов 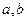, то есть .

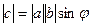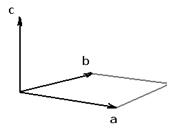
Таблица свойств скалярного и векторного произведений: сходство и различия.

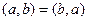
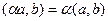
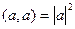
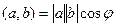
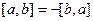
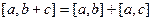
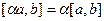
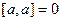
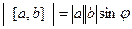
Метод нахождения векторного произведения с помощью определителя: Можно записать в 1-ю и 2-ю строку исходные два вектора, в третьей строке добавить произвольные обозначения осей 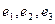, и вычислить этот определитель.

= .

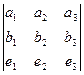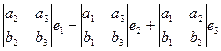Миноры порядка 2 будут координатами 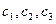нового вектора, который является векторным произведением.

Доказательство.

1) Получающийся таким образом вектор ортогонален двум исходным:

Если скалярно умножить на 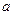, получим:

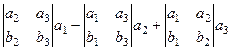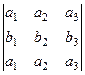= = 0.

Если скалярно умножить на 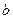, получим:

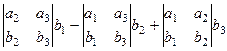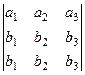= = 0.

Докажем также тот факт, что .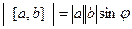

Квадрат модуля векторного произведения равен сумме квадратов миноров координат такого вектора: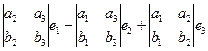

То есть величине =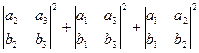

=

+
+ .

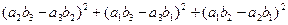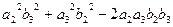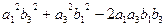
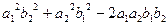В то же время = = = =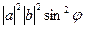

=

+ + +

.

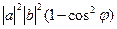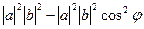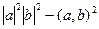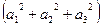
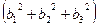
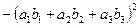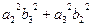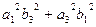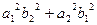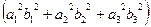
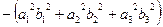
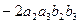
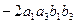
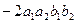Сократив то, что выделено в больших скобках, получаем одно и то же выражение.

- - - Перерыв - - -

Пример. Найти векторное произведение векторов (1,1,1) и (1,2,3)

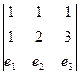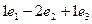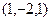= = . Ответ (1,-2,1).

Также можно проверить, что он действительно перпендикулярен исходным векторам (скалярно умножить на 1-й или на 2-й вектор, получим 0).

Примечание. Определитель можно вычислять либо разложением по 3-й строке, либо ранее известными методами, в том числе добавить копии двух первых столбцов справа.