Векторное построение геометрии

Имеется 2 основные аксиоматики геометрии: аксиоматика Гильберта(1899) и аксиоматика Вейля(1918), которую еще называют векторным построением геометрии. Основным элементом является вектор. Рассм. трехмерное векторное простр-воV₃ над полем R.Элементами V₃ явл. векторы a,b,x и т.д. Рассмотрим непустое мн-во Е, элементы которого будем называть точками и обозначать т.А, т.В. Рассмотрим отображение, которое каждой упорядоченной паре точек ставит в соответствие некоторый вектор, это отображение обозначим так: (А,В)→век(АВ) =век(х), т.А-начало, т.В-конец.

Мн-во Е наз-ся трехмерным евкл.простр-вом над в.п. V₃, если задано отображение (А,В)→век(АВ) =век(х) удовл. след.3требованиям:

1."т.АÎЕ "вект.хÎV₃ $!т.ВÎЕ | вект.х= век(АВ). Эта аксиома позволяет от одной т. отложить данный вект. единственным образом.

2."т.А,т.В,т.СÎЕ век-р(АВ)+век(ВС)=век(АС)(правилоΔдля сложения2век-ров).

3.В V₃ определено скалярное произведение векторов: век.а* век.b.

Трехм.евкл.простр-во будем обозн-ть Е₃. Требования1 и 2наз.аксиомами Вейля пр-ва Е₃. (Акс-ка Вейля насчитывает 19 аксиом)

Прямой ℓ, проходящей ч/з т.А и В наз. мн-во точек М,таких, что векторы АМ и АВ – коллинеарны (векторы v₁ , … , v_n Î V₃ (n ³ 1) называются коллинеарными, если существует прямая l и направленные отрезки(если у отрезка [AB] зафиксировать A-начало и B-конец, то получим понятие направленного отрезка) 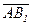, … , 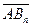Í l, что v_i = 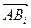(1 £ i £ n). В этом случае будем писать v₁ || v₂ || … || v_n–1 || v_n).

Плоскостью α, проходящей ч/з т. А,В,С наз. мн-во точек М, такое что векторы АМ, АВ,АС – коллинеарны.

Непротив-ти евкл. геом. Как известно, для док-ва евкл.геом. нужно построить какую-нибудь ее модель, т.е. нужно проверить непротивореч. акс. Вейля.

Пусть дано трехм.в.п. V₃ над полем R. Эл-тами его яв-ся векторы V₃ = {а,в,х,у…}. Рассм. мн-во Е, кот. совпадает с V₃: Е=V₃. Эл-ты мн-ва Е назовем точками Е={A, B,…}. Т.о., в той модели, кот. мы строим элемент имеет двойной смысл. Он одновременно яв-ся и точкой, и вектором. Т.о., т.А=вектору а и тд. Рассм. отображение (А,В)→вектор(АВ) =вектор(х), кот. опред-ся след. образом: (А,В)→ вектор(АВ) = вектор(х), = вектор В – вектор А.

Проверим выполнение акс. Вейля.

1. "т.АÎЕ "вект.хÎV₃ $!ВÎЕ вектор(АВ) =вектор(х), вектор В=вектор А+векторХ.

2.век-р(АВ)+век-р(ВС)=(векторВ-векторА)+(векторС-векторА)=векС-векА=век(АС)

Построенная модель аксиоматике Вейля. Полученная модель построена на основе алгебры, которая в свою очередь построена на базе арифметики. Т.о., доказана следующая фундаментальная теорема.

Т.Евклидова геометрия является непротиворечивой, если непротиворечива арифметика.

Др. словами, акс.Вейля позволяет решать задачи геом. векторным методом.

Пр. 1) Векторным методом док-ть теорему Пифагора.

2) Док-ть, что в любом параллелограмме d₁² + d₂² = 2a² + 2b².

МЕТОДИКА 28. Основные понятия: вектор, длина вектора, коллинеарные векторы; равные векторы, действия с векторами, скалярное произведение векторов. См. «Геометрия 7-11» §10 « Векторы на плоскости», «Векторы в пространстве».

Векторы в школьном курсе изучаются в геометрической и алгебраической(координатной) форме.

Смотрите «Геометрия 7-11», тема «Векторы на плоскости».

Векторный метод часто применяется при решении задач и доказательстве теорем.

В его применении можно выделить 3 этапа моделирования:

1) Формализация (перевод задачи на векторный язык);

2) Выполнение векторных преобразований;

3) Ответ на вопрос задачи: перевод с «векторного языка» на «язык», в терминах которого была сформирована задача.

Место в программе:

5-6 классы: пропедевтическое изучение — координатный луч, координатная прямая — изучается для изображения чисел и сравнения их, координатная плоскость, графики.

7-9 классы: алгебра — графики функций

геометрия: темы «Декартовы координаты на плоскости», «Векторы на плоскости».

10-11 классы: «Координаты и векторы в пространстве».

Требования к математической подготовке смотри в программе и в стандартах.

Основные типы задач :

Математические задачисвязаны с усвоением понятийного аппарата, с усвоением векторного метода. Например:

1) Записать координаты точки, координаты вектора.

2) Найти сумму векторов.

3) Найти угол между векторами.

4) Решить задачу векторным (координатным) методом.

Учебные задачи связаны сформированием компонентов векторного метода. Так для перевода задачи на «векторный язык» можно использовать специальные эвристики: прямые перпендикулярны, если скалярное произведение векторов, взятых на этих прямых, равно нулю и др.