Логический синтез одноразрядного четверичного сумматора


Одноразрядный четверичный сумматор - это комбинационное устройство, имеющее 5 входов (2 разряда одного слагаемого, 2 разряда второго слагаемого и вход переноса) и 3 выхода. Принцип работы ОЧС представлен с помощью таблицы истинности (табл.4).

Разряды обоих слагаемых закодированы : 0 - 00; 1 - 11; 2 - 10; 3 - 01.

Если ОЧС синтезируется для схемы 1-го типа, то в таблице истинности необходимо выделить 16 безразличных наборов, так как со старших выходов ОЧУ не могут прийти коды “2” и “3”. Если ОЧС синтезируется для схемы 2-го типа, то безразличные наборы в таблице истинности отсутствуют.

 

Таблица истинности ОЧС. Таблица 4.

a1 a2 b1 b2 p П S1 S2 Пример операции в четверичной с/с
0+0+0=00
0+0+1=01
х х х 0+3+0=03
х х х 0+3+1=10
х х х 0+2+0=02
х х х 0+2+1=03
0+1+0=01
Окончание табл. 4
a1 a2 b1 b2 p П S1 S2 Пример операции в четверичной с/с
0+1+1=02
3+0+0=03
3+0+1=10
х х х 3+3+0=12
х х х 3+3+1=13
х х х 3+2+0=11
х х х 3+2+1=12
3+1+0=10
3+1+1=11
2+0+0=02
2+0+1=03
х х х 2+3+0=11
х х х 2+3+1=12
х х х 2+2+0=10
х х х 2+2+1=11
2+1+0=03
2+1+1=10
1+0+0=01
1+0+1=02
х х х 1+3+0=10
х х х 1+3+1=11
х х х 1+2+0=03
х х х 1+2+1=10
1+1+0=02
1+1+1=03

Определим множество единичных кубов:

L = {01001, 01110, 01111, 10111}

и множество безразличных кубов:

N ={00010, 00011, 00100, 00101,

01010, 01011, 01100, 01101,

10010, 10011, 10100, 10101,

11010, 11011, 11100, 11101}.

Сформируем множество С0 = L U N.

Первым этапом алгоритма Рота является нахождение множества простых импликант. Для реализации этого этапа будем использовать операцию умножения (*) над множествами С0, С1 и т.д., пока в результате операции будут образовываться новые кубы большей размерности. Первый шаг умножения (С0*С0) приведен в табл. 5. В результате этой операции сформируем новое множество кубов:

С1 = {0001x, 0010x, 0101x, 010x1, 0110x, 0111x, 011x0, 011x1, 01x01, 01x10, 01x11, 0x010, 0x011, 0x100, 0x101, 1001x, 1010x, 101x1, 10x11, 1101x, 1110x, 1x010, 1x011, 1x100, 1x101, x0010, x0011, x0100, x0101, x1010, x1011, x1100, x1101}.

Множество Z0 кубов, не участвовавших в образовании новых кубов, пустое.

В табл. 6 приведен следующий шаг поиска простых импликант с помощью операции С1*С1. В результате образовалось множество С2 кубов второй размерности:

С2 = {011xx, 01x1x, 01xx1, 0x01x, 0x10x, 1x01x, 1x10x, x001x, x010x, x101x, x110x, xx010, xx011, xx100, xx101}.

Множество Z1 кубов, не участвовавших в образовании новых кубов:

Z1 = {101х1, 10х11}.

В табл. 7 приведен следующий шаг поиска простых импликант – операция С2*С2. В результате образовалось множество С3 кубов третьей размерности:

С3 = {хх01х, хх10х}.

Множество Z2 кубов, не участвовавших в образовании новых кубов:

Z2 = {011хх, 01х1х, 01хх1}.

Поиск простых импликант (С0*С0). Таблица 5.

        С0*С0
        -----                                      
          -----                                    
          0111x -----                                  
              -----                                
                -----                              
                0001x -----                            
                    -----                          
                    0010x -----                        
          01x10     0x010       -----                      
        010x1   01x11     0x011     0101x -----                    
          011x0         0x100       -----                  
        01x01   011x1         0x101     0110x -----                
                x0010               -----              
              10x11   x0011             1001x -----            
                    x0100               -----          
              101x1       x0101             1010x -----        
                        x1010       1x010       -----      
                          x1011       1x011     1101x -----    
                            x1100       1x100       -----  
                              x1101       1x101     1110x -----

 

 


 

Поиск простых импликант (С1*С1). Таблица 6.

  C1*C1 0001x 0010x 0101x 010x1 0110x 0111x 011x0 011x1 01x01 01x10 01x11 0x010 0x011 0x100 0x101 1001x 1010x 101x1 10x11 1101x 1110x 1x010 1x011 1x100 1x101 x0010 x0011 x0100 x0101 x1010 x1011 x1100
  0001x -----                                                              
  0010x   -----                                                            
  0101x 0x01x   -----                                                          
  010x1       -----                                                        
  0110x   0x10x     -----                                                      
  0111x     01x1x   011xx -----                                                    
  011x0             -----                                                  
  011x1       01xx1     011xx -----                                                
  01x01                 -----                                              
  01x10                   -----                                            
  01x11                 01xx1 01x1x -----                                          
  0x010                       -----                                        
  0x011                       0x01x -----                                      
  0x100                           -----                                    
  0x101                           0x10x -----                                  
  1001x x001x                             -----                                
  1010x   x010x                             -----                              
  101x1                                   -----                            
  10x11                                     -----                          
  1101x     x101x                         1x01x       -----                        
  1110x         x110x                       1x10x       -----                      
  1x010                       xx010                   -----                    
  1x011                         xx011                 1x01x -----                  
  1x100                           xx100                   -----                
  1x101                             xx101                 1x10x -----              
  x0010                                                   -----            
  x0011                                                   x001x -----          
  x0100                                                       -----        
  x0101                                                       x010x -----      
  x1010                                                   xx010       -----    
  x1011                                                     xx011     x101x -----  
  x1100                                                       xx100       -----
  x1101                                                         xx101     x110x

 


Поиск простых импликант (С2*С2). Таблица 7.

  C2*C2 011xx 01x1x 01xx1 0x01x 0x10x 1x01x 1x10x x001x x010x x101x x110x xx010 xx011 xx100 xx101
  011xx -----                            
  01x10   -----                          
  01xx1     -----                        
  0x01x       -----                      
  0x10x         -----                    
  1x01x       xx01x   -----                  
  1x10x         xx10x   -----                
  x001x               -----              
  x010x                 -----            
  x101x               xx01x   -----          
  x110x                 xx10x   -----        
  xx010                       -----      
  xx011                       xx01x -----    
  xx100                           -----  
  xx101                           xx10x -----

 

 

Поиск простых импликант (С3*С3). Таблица 8.

  C3*C3 xx01x xx10x
  xx01x -----  
  xx10x   -----

 

Результат С3*С3 приведен в табл. 8. Новых кубов (четвертой размерности) не образовалось. Получено множество Z3 = {хх01х, хх10х}.

На этом заканчивается этап поиска простых импликант, так как |С4|£1. Множество простых импликант

Z = Z0UZ1UZ2UZ3 = {101х1, 10х11, 011хх, 01х1х, 01хх1, хх01х, хх10х}.

Следующий этап – поиск L-экстремалей на множестве простых импликант. Для этого используется операция # (решетчатое вычитание). В табл. 9 из каждой простой импликанты поочередно вычитаются все остальные простые импликанты Z#(Z\z), результат операции (последняя строка таблицы) указывает на то, что L-экстремалями стали следующие простые импликанты:

E = 01xx1, xx01x, xx10x.

Необходимо проверить, нет ли среди них таких, которые стали L-экстремалями за счет безразличных кубов. Для этого в табл. 10 из кубов множества L вычитаются остатки простых импликант, полученные в табл. 9 (результат выполнения операции Z#(Z\z)). По результатам табл. 10 L-экстремалью, не связанной с безразличными наборами, стал куб 01хх1 (остаток от вычитания из него всех остальных простых импликант – 01001 – относится ко множеству единичных наборов L исходного задания функции). Этот куб обязательно должен войти в минимальное покрытие.

Поиск L-экстремалей. Таблица 9.

  Z#(Z\z) 101x1 10x11 011xx 01x1x 01xx1 xx01x xx10x
  101x1 -----   zz0zz yyzz0 011xx yy0z0 01x1x yy0zz 01xx1 01yz0 xx01x 01zz0 0x01x x110x xx100
  10x11 zzz0z ----- yyz00 011xx yyzz0 01x1x yyz0z 01xx1 01zz0 0x01x x101x xx010 y1zy0 0yzy0 01zyy 0x10x x110x xx100
  011xx yyzzz yyyzz ----- zz0zz 0101x zz0zz 010x1 z0yzz 1zyzz 10yzz 0x01x x101x xx010 z0zzz 0010x 1zzzz 1110x 10zzz 1x100   x0100
  01x1x yyzyz yyyzz zzz0z 0110x ----- zzz0z z0zzz 0001x 1zzzz 1101x 10zzz 1x010 x0010 zyzyz 0010x yzzyz 1110x y0zyz 1x100 1yzyz x0100
  01xx1 yyzzz yyzzz zzzz0 zzzz0 ----- zyzz0 0001x yzzz0 1101x y0zzy 1x010 1yzzy x0010 zyzz0 0010x yzzz0 1110x y0zzy 1x100 1yzzy x0100
  xx01x zzyyz zzzzz zzyyz zzzzz zzzyz ----- ----- ----- ----- zzyyz 0010x zzyyz 1110x zzyyz 1x100 zzyyz x0100
  xx10x zzzzz   zzzzz   zzyzz zzyyz 0001x zzyyz 1101x zzyyz 1x010 zzyyz x0010 ----- ----- ----- -----

Проверка L-экстремалей. Таблица 10.

  L ∩ Ê
 
  0001x
  1101x
  1x010
  x0010
  0010x
  1110x
  1x100
  x0100

Далее необходимо проанализировать, какие из исходных единичных кубов (множество L) не покрыты найденной L-экстремалью. Этот анализ осуществляется с помощью табл. 11.

Поиск непокрытых исходных наборов. Таблица 11.

  L # E
  01xx1 zzzzz zzzzy zzzzz yyzzz

Из табл. 11 видно, что L-экстремалью не покрыты два единичных куба (01110 и 10111 ). Чтобы их покрыть, воспользуемся множеством простых импликант, не являющихся L-экстремалями (табл.12).

Покрытие оставшихся кубов. Таблица 12.

  L ∩ Ž
  101x1
  10x11
  011xx
  01x1x
  xx01x
  xx10x

Из табл. 12 видно, что каждый из непокрытых единичных кубов может быть покрыт двумя равнозначными способами. Следовательно, существуют 4 тупиковые (минимальные) формы:

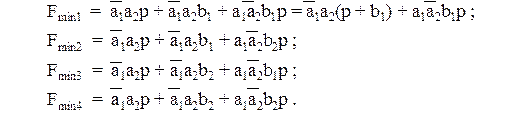Функциональную схему ОЧС (рис. 7) построим по Fmin1 :

 

 


Дата добавления: 2022-02-05; просмотров: 271;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.024 сек.