Алгоритмы вычисления линейных и круговых сверток

9.1.1. Дискретная линейная свертка

Во временной области соотношение вход-выход ЛДС в случае использования импульсной характеристики может быть описано формулой дискретной линейной свертки:

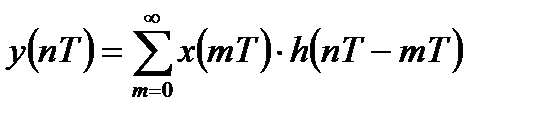. (9.1)

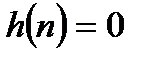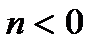Для физически реализуемой системы импульсная характеристика при , поэтому выражения для дискретной линейной свертки за счет замены верхнего индекса суммирования на 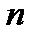изменятся следующим образом:

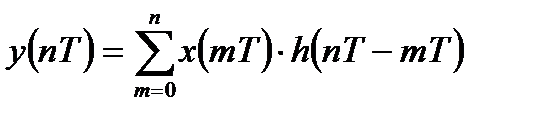. (9.3)

Если последовательност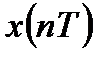и и 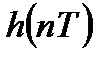являются конечными с длительностям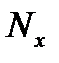и и 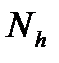, то выходная последовательность 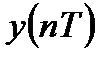также является конечной с длительностью:

.

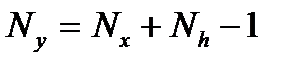Например, при использовании в качестве входного сигнала единичного импульса длительностью 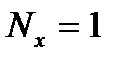как и ожидалось, длительность выходного сигнала определяется длительностью импульсной характеристики: .

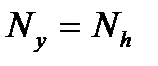Соответственно, линейная свертка конечных последовательностей с длинам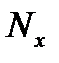и и 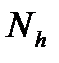определяется выражением:

, .

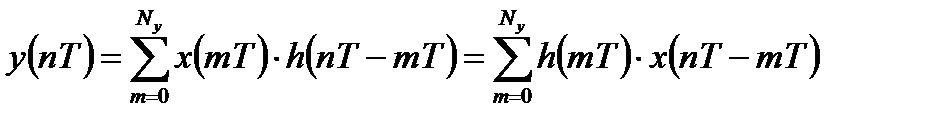где .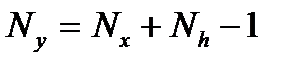

Рисунок 9.1 – линейная свертка конечных последовательностей

9.1.2. Цифровая обработка сигналов в частотной области

Алгоритмы дискретной линейной свертки применяются только для коротких последовательностей. Для дискретных сигналов с сотнями и более отсчетов, возникает проблема сокращения вычислительных затрат.

Сокращение вычислительных затрат достигается за счет цифровой фильтрации сигналов в частотной области и использования быстрых алгоритмов БПФ и ОБПФ.

Алгоритм фильтрации в частотной области записывается следующим образом:

1. Конечная последовательность отсчетов входного сигнала 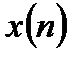и импульсная характеристика фильтра 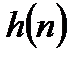дополняются нулями так, чтобы длины последовательностей стали равными.

2. Вычисляются ДПФ дополненных нулями последовательностей с результатами в виде 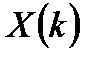и .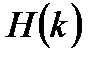

3. Вычисленные ДПФ поэлементно умножаются для приближенной реализации умножения спектра входного сигнала на частотную характеристику фильтра:

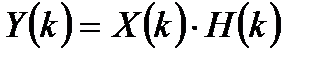
(приближенная реализация, так как непрерывные спектр и частотная характеристика дискретных сигналов заменяются дискретными отсчетами ДПФ).

4. Вычисляется ОДПФ от результата перемножения:

.

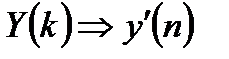Для снижения вычислительных затрат при вычислении ДПФ входного сигнала и при обратном преобразовании во временную область целесообразно использовать алгоритмы БПФ и обратного БПФ (ОБПФ). Блок-схема алгоритма фильтрации в частотной области представлена на рисунке 9.3.

Рисунок 9.3 – Блок-схема алгоритма обработки в частотной области