Алгоритмы для расчета кинематики групп Ассура
Аналитический расчет основан на методе векторного замкнутого контура. Условимся для замыкания контура группы использовать вектор 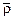 , который проводим из центра кинематической пары Bв центр кинематической пары D для групп первого и третьего видов (см. рис. 3.1); из центра кинематической пары Bв точку D0 на оси поступательной пары для групп второго и пятого видов; из точки B0в точку D0для группы четвертого вида. Так как входы в группы должны быть заданы (табл. 3.1–3.3), то этот вектор
, который проводим из центра кинематической пары Bв центр кинематической пары D для групп первого и третьего видов (см. рис. 3.1); из центра кинематической пары Bв точку D0 на оси поступательной пары для групп второго и пятого видов; из точки B0в точку D0для группы четвертого вида. Так как входы в группы должны быть заданы (табл. 3.1–3.3), то этот вектор 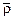 всегда известен своими проекциями на оси X0,Y0, известны также первые и вторые производные от проекций.
всегда известен своими проекциями на оси X0,Y0, известны также первые и вторые производные от проекций.
3.2.1. Решение задачи о положениях группы 21
Исходные данные:
а) переменные (вход) – первая строка табл. 3.1;
б) постоянные – первая строка табл. 3.4.
Уравнение замкнутости контураBCD
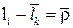 (3.1)
(3.1)
¨ в проекциях на оси X0Y0имеет вид
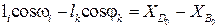 ,
,
(3.2)
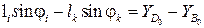 .
.
Исключая угол 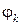 и одновременно вводя обозначения:
и одновременно вводя обозначения:
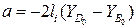 ;
; 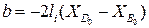 ;
;
(3.3)
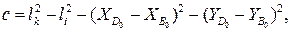
получим трансцендентное уравнение:
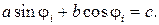 (3.4)
(3.4)
Это уравнение при помощи подстановки 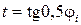 приводится к алгебраическому. Его решение:
приводится к алгебраическому. Его решение:
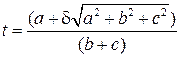 , (3.5)
, (3.5)
где δ –коэффициент, учитывающий сборку группы. Проверяем значение коэффициента δ: если группа расположена слева от вектора 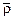 , то δ= –1, если справа – δ = +1 (пунктирные линии на рис. 3.1).
, то δ= –1, если справа – δ = +1 (пунктирные линии на рис. 3.1).
Далее получим:
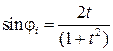 ;
; 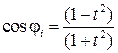 . (3.6)
. (3.6)
С учетом (3.2) получим:
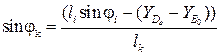 ,
,
(3.7)
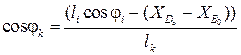 .
.
3.2.2. Решение задачи о скоростях группы 21
Исходные данные:
а) переменные (вход) – первая строка таблицы 3.2;
б) постоянные – те же, что и в задаче о положениях.
Дифференцируем (3.2):
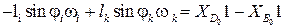 ,
,
(3.8)
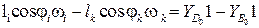 .
.
Получена система двух уравнений с двумя неизвестными ωi, ωk коэффициенты и свободные члены которой имеют вид:
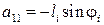 ;
; 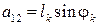 ;
;
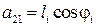 ;
; 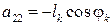 ; (3.9)
; (3.9)
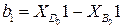 ;
; 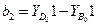 .
.
Решая систему, найдем угловые скорости звеньев:
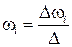 ,
,  , (3.10)
, (3.10)
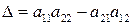 ;
; 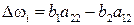 ; (3.11)
; (3.11)
где  .
.
3.2.3. Решение задачи об ускорениях группы 21
Исходные данные:
а) переменные (вход) – первая строка таблицы 3.3;
б) постоянные – те же.
Дифференцируем (3.8):
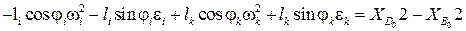 ,
,
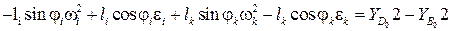 . (3.12)
. (3.12)
Снова получена система двух уравнений с двумя неизвестными 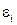 ,
, 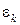 . Коэффициенты при неизвестных останутся прежними (3.10), но изменятся свободные члены:
. Коэффициенты при неизвестных останутся прежними (3.10), но изменятся свободные члены:
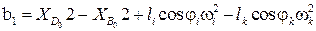 ,
,
(3.13)
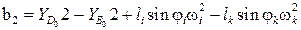 .
.
Решая систему, получим угловые ускорения звеньев.
3.2.4. Решение задачи о положениях группы 22
Исходные данные:
а) переменные (вход) – вторая строка таблицы 3.1;
б) постоянные – вторая строка таблицы 3.4.
Уравнение замкнутости контура BCDD0:
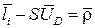 , (3.14)
, (3.14)
¨ где S – расстояние от точки D0 до точки D.
Проектируем на оси X0Y0:
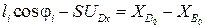 ,
,
(3.15)
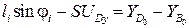 .
.
Исключая угол 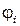 , получим квадратное уравнение
, получим квадратное уравнение
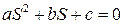 , (3.16)
, (3.16)
где  ;
; 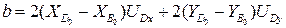 ; (3.17)
; (3.17)
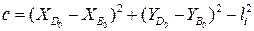 .
.
Решение уравнения:
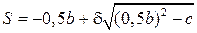 , (3.18)
, (3.18)
где 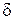 – коэффициент, учитывающий сборку группы. Проверкой убеждаемся в выборе значения коэффициента
– коэффициент, учитывающий сборку группы. Проверкой убеждаемся в выборе значения коэффициента 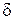 . Мысленно переносим вектор
. Мысленно переносим вектор 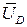 в точку В: если он с вектором
в точку В: если он с вектором 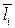 образует острый угол, то
образует острый угол, то 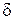 = +1, если тупой,
= +1, если тупой, 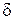 = –1 (пунктирные линии на рис. 3.1).
= –1 (пунктирные линии на рис. 3.1).
С учетом (3.2) найдем:
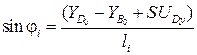 ,
,
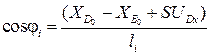 . (3.19)
. (3.19)
3.2.5. Решение задачи о скоростях группы 22
Исходные данные:
а) переменные (вход) – вторая строка таблицы 3.2;
б) постоянные – те же.
Дифференцируем (3.15):
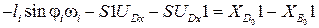 ,
,
(3.20)
 .
.
Получена система двух уравнений с двумя неизвестными ωi, S1. Коэффициенты и свободные члены системы:
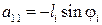 ;
;  ;
;
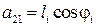 ;
; 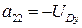 ; (3.21)
; (3.21)
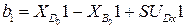 ;
; 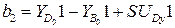 .
.
Решая систему, получим угловую скорость ωi и относительную скорость S1.
3.2.6. Решение задачи об ускорениях группы 22
Исходные данные:
а) переменные (вход) – вторая строка таблицы 3.3;
б) постоянные – те же.
Дифференцируем (3.20):
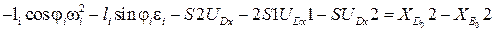 ,
,
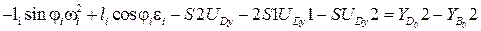 . (3.22)
. (3.22)
Снова получим систему двух уравнений с двумя неизвестными 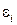 , S2. Коэффициенты системы остались прежними (3.21), свободные члены изменились и имеют вид:
, S2. Коэффициенты системы остались прежними (3.21), свободные члены изменились и имеют вид:
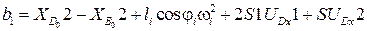 ,
,
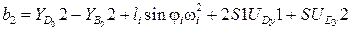 .
.
Решая систему, получим угловое ускорение 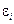 и относительное ускорение S2.
и относительное ускорение S2.
3.2.7. Решение задачи о положениях группы 23
Исходные данные:
а) переменные (вход) – третья строка таблицы 4.1;
б) постоянные – третья строка таблицы 4.4.
Уравнение замкнутости контура BDB:
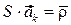 , (3.23)
, (3.23)
где S – расстояние от точки D до точки С.
В проекциях на оси:
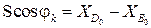 ,
,
(3.24)
 .
.
Исключая угол 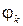 , получим:
, получим:
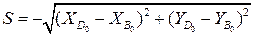 . (3.25)
. (3.25)
С учетом (3.24) найдем:
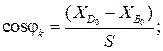
(3.26)
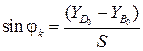 .
.
3.2.8. Решение задачи о скоростях группы 23
Исходные данные:
а) переменные (вход) – третья строка таблицы 3.2;
б) постоянные – третья строка таблицы 3.4.
Дифференцируем (3.24):
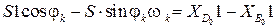 ,
,
(3.27)
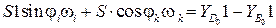 .
.
Коэффициенты и свободные члены системы (3.27):
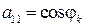 ;
; 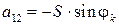 ;
;
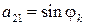 ;
; 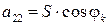 ; (3.28)
; (3.28)
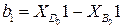 ;
; 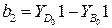 .
.
Решая систему, найдем относительную скорость S1 и угловую скорость 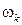 .
.
3.2.9. Решение задачи об ускорениях группы 23
Исходные данные:
а) переменные (вход) – третья строка таблицы 3.3;
б) постоянные – те же.
Дифференцируем (3.27):
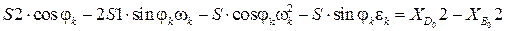 ,
,
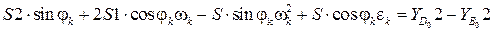 (3.29)
(3.29)
Коэффициенты системы (3.29) остаются прежними (3.28), свободные члены вычисляются из выражений
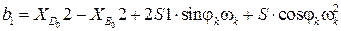 ,
,
(3.30)
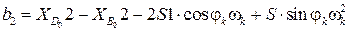
Решая систему, получим относительное ускорение S2 и угловое ускорение 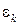 .
.
3.2.10. Решение задачи о положениях группы 24
Исходные данные:
а) переменные (вход) – четвертая строка таблицы 3.1;
б) постоянные – четвертая строка таблицы 3.4.
Уравнение замкнутости контураB0CD0:
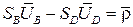 . (3.31)
. (3.31)
В проекциях на оси:
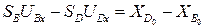 ,
,
(3.32)
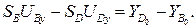
Получена система двух уравнений с двумя неизвестными SB, SD.
Коэффициенты и свободные члены системы:
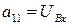 ;
; 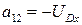 ;
; 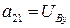 ;
; 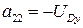 ;
;
(3.33)
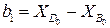 ;
; 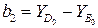 .
.
Решая систему, найдем перемещения SB, SD, отсчитываемые от точек B0, D0.
3.2.11. Решение задачи о скоростях группы 24
Исходные данные:
а) переменные (вход) – четвертая строка таблицы 3.2;
б) постоянные – те же.
Дифференцируем (3.32):
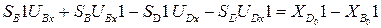 ,
,
(3.34)
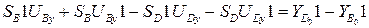 .
.
Свободные члены системы (3.34):
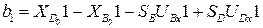 ,
,
(3.35)
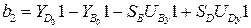 .
.
Коэффициенты остались прежними (3.33). Решая систему, найдем SB1, SD1.
3.2.12. Решение задачи об ускорениях группы 24
Исходные данные:
а) переменные (вход) – четвертая строка таблицы 3.3;
б) постоянные – те же.
Дифференцируем (3.34):
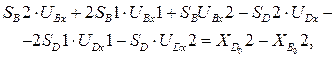 (3.36)
(3.36)
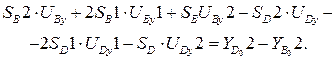
Свободные члены системы (3.36):
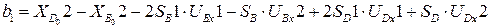 ,
,
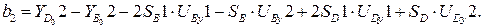 (3.37)
(3.37)
Коэффициенты вычисляются из (3.33). Решая систему, найдем относительные ускорения SB2, SD2.
3.2.13. Решение задачи о положениях группы 25
Исходные данные:
а) переменные (вход) – пятая строка таблицы 3.1;
б) постоянные – пятая строка таблицы 3.4.
Уравнение замкнутости контураD0DB:
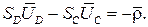 (3.38)
(3.38)
В проекциях на оси X0Y0:
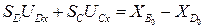 ,
,
(3.39)
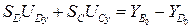 .
.
Коэффициенты и свободные члены системы:
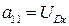 ;
; 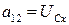 ;
; 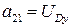 ;
; 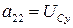 ;
;
(3.40)
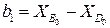 ;
; 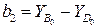 .
.
Решая систему (3.39), найдем SD, SC. Проекции вектора 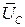 выражаются через проекции вектора
выражаются через проекции вектора 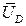 и угол
и угол 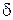 ,которые входят в исходные данные:
,которые входят в исходные данные:
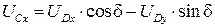 ,
,
(3.41)
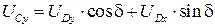 .
.
3.2.14. Решение задачи о скоростях группы 25
Исходные данные:
а) переменные (вход) – пятая строка таблицы 3.2;
б) постоянные – те же.
Дифференцируем (3.39):
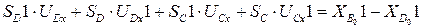 , (3.42)
, (3.42)
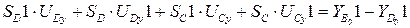 .
.
Свободные члены системы (3.42):
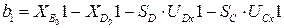 ;
;
(3.43)
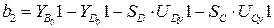 .
.
Коэффициенты сохраняют свои значения и вычисляются из (3.40).
Решая систему, найдем относительные скорости SD1, SC1. Входящие в уравнение (3.43) величины 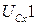 ,
, 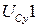 найдем дифференцированием уравнения (3.41):
найдем дифференцированием уравнения (3.41):
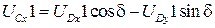 ,
,
(3.44)
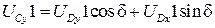 .
.
3.2.15. Решение задачи об ускорениях группы 25
Исходные данные:
а) переменные (вход) – пятая строка табл. 3.3;
б) постоянные – те же.
Дифференцируем (3.43):
 (3.45)
(3.45)
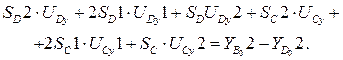
Выделим свободные члены системы (3.45):
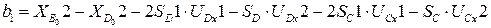 ,
,
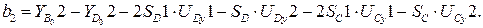 (3.46)
(3.46)
Коэффициенты вычисляются из (3.40). При решении системы найдем относительные ускорения SD2, SC2. Входящие в (3.45)  ,
, 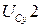 величины найдем дифференцированием (3.44):
величины найдем дифференцированием (3.44):
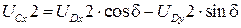 ;
; 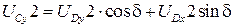 .
.
Дата добавления: 2020-07-18; просмотров: 862;











