В гармонический ряд Фурье
Из курса математики известно, что любая периодическая функция времени f(t), удовлетворяющая условиям Дирихле, может быть представлена гармоническим рядом Фурье:
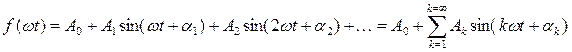 .
.
Здесь А0 – постоянная составляющая, 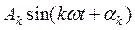 - k-я гармоническая составляющая или сокращенно k-я гармоника. 1-я гармоника называется основной, а все последующие - высшими.
- k-я гармоническая составляющая или сокращенно k-я гармоника. 1-я гармоника называется основной, а все последующие - высшими.
Амплитуды отдельных гармоник Ак не зависят от способа разложения функции f(t) в ряд Фурье, в то же время начальные фазы отдельных гармоник 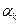 зависят от выбора начала отсчета времени (начала координат).
зависят от выбора начала отсчета времени (начала координат).
Отдельные гармоники ряда Фурье можно представить в виде суммы синусной и косинусной составляющих:
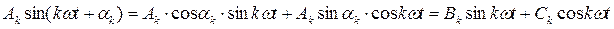 .
.
Тогда весь ряд Фурье получит вид:
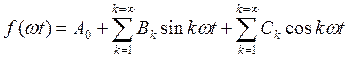 .
.
Соотношения между коэффициентами двух форм ряда Фурье имеют вид:
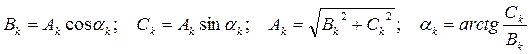 .
.
Если k-ю гармонику и ее синусную и косинусную составляющие заменить комплексными числами, то соотношение между коэффициентами ряда Фурье можно представить в комплексной форме:
 .
.
Если периодическая несинусоидальная функция времени задана (или может быть выражена) аналитически в виде математического уравнения, то коэффициенты ряда Фурье определяются по формулам, известным из курса математики:
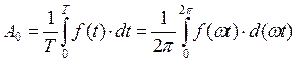 ,
,
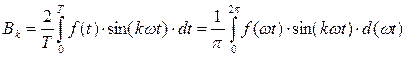 ,
,
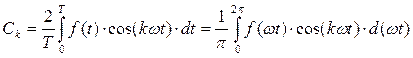 ,
,
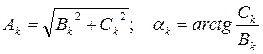 .
.
На практике исследуемая несинусоидальная функция f(t) обычно задается в виде графической диаграммы (графически) (рис. 118) или в виде таблицы координат точек (таблично) в интервале одного периода (табл. 1). Чтобы выполнить гармонический анализ такой функции по приведенным выше уравнениям, ее необходимо предварительно заменить математическим выражением. Замена функции, заданной графически или таблично математическим уравнением, получила название аппроксимации функции.

Т а б л и ц а 1
| m | … | … | … | … | M | ||||
| tm | t0 | t1 | t2 | t3 | … | … | … | … | T |
| fm | f0 | f1 | f2 | f3 | … | … | … | … | f0 |
В настоящее время гармонический анализ несинусоидальных функций времени f(t) выполняется, как правило, на ЭВМ. В простейшем случае для математического представления функции применяется кусочно-линейная аппроксимация. Для этого вся функция в интервале одного полного периода разбивается на M=20-30 участков так, чтобы отдельные участки были по возможности ближе к прямым линиям (рис. 1). На отдельных участках функция аппроксимируется уравнением прямой fm(t)=am+bm××t, где коэффициенты аппроксимации (am, bm) определяются для каждого участка через координаты его конечных точек, например, для 1-го участка получим:
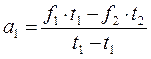 ;
; 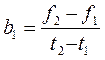 .
.
Период функции Т разбивается на большое число шагов интегрирования N, шаг интегрирования 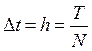 , текущее время ti=h×i, где i - порядковый номер шага интегрирования. Определенные интегралы в формулах гармонического анализа заменяются соответствующими суммами, их подсчет выполняется на ЭВМ по методу трапеций или прямоугольников, например:
, текущее время ti=h×i, где i - порядковый номер шага интегрирования. Определенные интегралы в формулах гармонического анализа заменяются соответствующими суммами, их подсчет выполняется на ЭВМ по методу трапеций или прямоугольников, например:
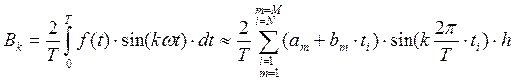 .
.
Для определения амплитуд высших гармоник с достаточной точностью 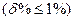 число шагов интегрирования должно составлять не менее 100k, где k - номер гармоники.
число шагов интегрирования должно составлять не менее 100k, где k - номер гармоники.
В технике для выделения отдельных гармоник из несинусоидальных напряжений и токов применяют специальные приборы, называемые гармоническими анализаторами.
Дата добавления: 2020-07-18; просмотров: 743;











