Дискретная свертка сигналов

В теории цифровой обработки сигналов важное значение имеет дискретная свертка. По аналогии со сверткой двух непрерывных сигналов u(t) и x(t)

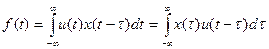
вводят линейную дискретную свертку, представляющую собой вещественный (действительный) дискретный канал, отсчеты которого связаны с отчетами двух вещественных дискретных сигналов {u_k} и {x_m} соотношением

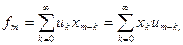m =0, 1, 2, ... . (9.22)

Отметим, что суммирование по номерам ведется от k = 0, поскольку исследуются вещественные сигналы. Число выходных отсчетов в свертке

N = k + m – 1.

ПРИМЕР 9.6. Для двух дискретных сигналов, заданных соответственно отсчетами {u_k} = {1, 2, 3, 4, 5} и {h_m} = {10, 7, 5, 3}, вычислить дискретную свертку.

Р е ш е н и е. Воспользовавшись алгоритмом дискретной свертки (9.22), осуществим непосредственное вычисление ее отсчетов. Для наглядности на одной полоске клетчатой бумаги запишем отсчеты сигнала {u_k}, а на другой – отсчеты другого сигнала {h_m}, причем элементы второго сигнала расположены «зеркально», т.е. справа налево (Рис. 9.12).

Для того, чтобы определить нулевой отсчет свертки, совместим первые позиции сигналов (Рис. 9.12, б). и перемножим отсчеты, находящиеся друг под другом. В результате имеем у₀ = 10. Для вычисления следующего отсчета у₁ сдвинем любую полоску на одну позицию (Рис. 9.12, в). В данном случае, после перемножения отсчетов и сложения результатов, получим у₁ = 20 + 7 = 27.

Проделав аналогичные операции до момента, когда отсчеты перестанут накладываться, находим значения свертки:

{y_k} = {10, 27, 49, 74, 99, 64, 37, 15},